Complexidade
O que é Complexidade?
Em linhas gerais, a complexidade de tempo de um algoritmo é o quanto as variáveis de entrada impactam no seu tempo de execução.
Para se referir a complexidade de um algoritmo, se usa a notação Big O, denotada por O(N). A notação Big O tem o seguinte significado: No pior caso da execução deste algoritmo, o número de operações realizado será proporcional a N, e por simplicidade, eliminamos constantes e fatores não dominantes. A quantidade de operações que os computadores atuais executam em um segundo é por volta de 10^8, portanto podemos estimar o tempo de execução de um programa usando análise de complexidade. Basta fazer o cálculo de complexidade e dividir por 10^8, e a resposta será aproximadamente o tempo de execução em segundos. Esse mesmo conceito se extende a memória utilizada por um programa, podemos fazer o cálculo de complexidade e dividir o resultado por 10^6, e saberemos quantos MegaBytes serão utilizados pelo programa no pior caso.
Exemplos:
printf("Hello World\n");
Esse código tem complexidade O(1) (também chamado de complexidade constante), porque nenhuma variável de entrada impacta no seu tempo de execução. A complexidade de memória também é O(1).
Loops
int n;
scanf("%d",&n);
for(int i = 0; i < n; i++){
printf("%d\n",i);
}
Esse código tem complexidade O(n), pois o seu tempo tempo de execução cresce linearmente dependendo da variável n. A memória necessária não depende de nenhuma variável de entrada então é O(1).
int n;
scanf("%d",&n);
for(int i = 0; i < 10*n; i++){
printf("%d\n",i);
}
Esse código também tem complexidade O(n), porque eliminamos os fatores constantes para manter a simplicidade. Complexidade de memória O(1).
int n,m;
scanf("%d %d",&n,&m);
for(int i = 0; i < n; i++){
printf("%d\n",i);
}
for(int i = 0; i < m; i++){
printf("%d\n",i);
}
Muitas vezes, a complexidade depende de mais de uma variável de entrada. Como não temos nenhuma informação sobre o significado das variáveis, a complexidade é O(n+m). Se soubéssemos por exemplo que m fosse sempre muito maior que m, poderíamos dizer O(m). Mais uma vez a memória utilizada não depende de nenhuma variável de entrada.
Multiplicação de matrizes
O código abaixo computa C = A * B, onde A é uma matriz n por p e B é uma matriz p por m.
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
C[i][j] = 0;
for(int k = 0; k < p; k++){
C[i][j] += A[i][k] * B[k][j];
}
}
}
Como os fors estão aninhados a complexidade do código é a multiplicação das complexidades de cada for, sendo então, O(n*m*p). A multiplicação produz a matriz C como resultado, que tem dimenções n por m, Como é necessário alocar esse espaço, a complexidade de memória é O(n*m).
Ordenação
Um problema bastante estudado é o de ordenação. Existem vários algoritmos resolvem o problema eficientemente, não será mostrado um desses. O código a seguir ordena um vetor v de tamanho n.
for(int i = 0; i < n; i++){
for(int j = i; j < n; j++){
if(v[i] > v[j]){
tmp = v[i];
v[i] = v[j];
v[j] = tmp;
}
}
}
A quantidade de vezes que o segundo loop executa depende do i, então é um pouco mais difícil de analisar a complexidade.
Ao longo das iterações do primeiro loop, a quantidade de iterações do segundo é n + (n-1) + (n-2) + (n-3) + ... + 1, ou seja, é soma de PA e podemos resolver para O((n+1)*n/2). Em análise de complexidade só nos importamos com quando as variáveis são muito grandes(tendem a infinito), de um modo bem bruto infinito e infinito/2 dá no mesmo, então podemos escrever a complexidade como O((n+1)*n). Novamente quando pensamos em números bem altos n e n+1 se tornam praticamente a mesma coisa e podemos concluir que a complexidade é O(n^2).
Portanto podemos dizer que a complexidade do código acima é O((n+1)*n/2), O((n+1)*n) ou O(n^2). Mas geralmente optamos pela forma mais simples que é O(n^2).
A intuição sobre a complexidade de memória pode acabar te enganando nesse exemplo. O motivo é o seguinte: o código apenas troca os valores de lugar dentro do vetor, não sendo necessário alocar um novo vetor com a resposta(Ao contrário da multiplicação de matrizes), então a complexidade de memória é O(1).
Recursão
Também é possível analisar a complexidade de funções recursivas.
Exponenciação
int slow_exp(int base, int e){
if(e == 0)
return 1;
return base * slow_exp(base,e-1);
}
Nessa função, em cada chamada, o expoente decresce em um, atingindo o caso base quando se iguala a 0. Então são feitas O(n) chamadas. Quando avaliamos complexidade de memória de funções recursivas, temos que levar em conta a pilha de execução também. São empilhadas n chamadas na pilha, então a complexidade de memória é O(n).
Exponenciação rápida
int fast_exp(int base, int e){
if(e == 0)
return 1;
if(e % 2)
return base * fast_exp(base * base,e/2);
else
return fast_exp(base * base, e/2);
}
Essa é uma função que também computa uma exponenciação. É um bom exemplo de como problemas abordados de forma diferente ou usando propriedades matemáticas podem ser resolvidos de forma mas eficiente. Em cada chamada na recursão, o expoente é dividido por 2, atingindo o caso base quando se iguala a 0. É fácil ver que o número 2^k levaria k chamadas para atingir o caso base, isso ocorre porque log2 (2^k) = k, então a complexidade é O(log N). A complexidade de memória é justificada da mesma forma que no caso anterior, a memória utilizada será o número de chamadas recursivas, então, O(log n).
Fibonacci
int fibonacci(int n){
if(n == 0)
return 0;
if(n == 1)
return 1;
return fibonacci(n-1) + fibonacci(n-2);
}
A famosa função de fibonacci. Essa função recursiva é bem bonita de se ver declarada, mas não é nada eficiente.
Pense que queremos Calcular Fibonacci(7)
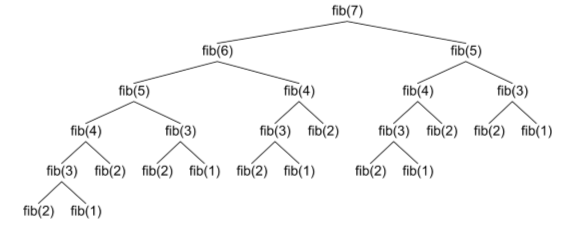
Essa a árvore formada pelas chamadas recursivas, olhe quantas vezes recomputamos as mesmas coisas. A complexidade dessa função é O(2^n), pois para cada chamada de fibonacci recursiva, fazemos outras duas, e acabamos recomputando várias vezes as mesmas coisas. Implemente essa função em sua máquina e faça uma chamada de fibonacci(40), já deve ser possível sentir o tempo que o programa leva para processar isso.
A complexidade de memória dessa função pode ser um pouco mais complicada de analisar vamos por partes. No total, serão feitos O(2^n) chamadas recursivas, e todas elas precisaram de um espaço na pilha de execução, no entanto, as 2^n chamadas não coexistirão na pilha de execução. Olhando bem atentamente e seguindo o fluxo das chamadas recursivas, é possível ver que no máximo um ‘ramo’ da árvore estará na pilha por vez, o ramo mais longo tem comprimento n portanto, complexidade de memória O(n).
VideoAulas Complementares
https://www.youtube.com/watch?v=YoZPTyGL2IQ (12 min.)
https://www.youtube.com/watch?v=moPtwq_cVH8 (51 min. MIT)