Subsecções de ED Linear
Pilha
A pilha é uma estrutura que, como o nome sugere, permite inserção e remoção apenas do “topo”. Isto significa que, ao remover um elemento da pilha, o elemento a ser removido é o último que foi inserido. Também é conhecido como LIFO (last-in first-out).
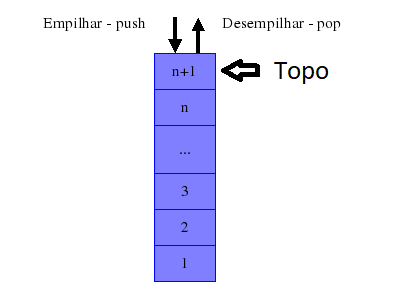
Métodos:
push- Insere um elemento na pilha.pop- Remove o elemento do topo da pilha.top- Retorna o elemento do topo da pilha.size- Retorna o tamanho da pilha.empty- Retorna true se estiver vazia, se não, retorna falso.
Exemplo
- Programa simples que vai inserir elementos na pilha e depois conforme for removendo, printa cada elemento
#include <bits/stdc++.h>
using namespace std;
int main() {
stack<int> pilha; // construtor, entre <> deve ser inserido o tipo de dado que será armazenado
pilha.push(2); // o metodo push insere o elemento no topo da pilha
pilha.push(7);
pilha.push(8);
pilha.push(4);
cout << pilha.size() << endl; // tamanho da pilha
// enquanto não estiver vazia, remove o elemento do topo e printa ele
while(!pilha.empty()){
int elemento = pilha.top();
cout<<elemento<<" ";
pilha.pop();
}
return 0;
}
Saída
4 8 7 2
Pilha de Mínimo
E se quisermos o seguinte problema:
- Dado N números em uma pilha, para os últimos Q números na pilha, printe o menor número em toda pilha até então.
Podemos fazer um código que para cada Q últimos números na pilha, podemos ir percorrendo toda a pilha restante, salvando os menores, sem alterar a pilha atual.
#include <bits/stdc++.h>
using namespace std;
int main(){
stack<int> st;
st.push(5);
st.push(3);
st.push(8);
st.push(1);
st.push(7);
stack<int> st_aux;
// para os 4 últimos números, printe o menor número de toda a pilha até ele
for(int q=0; q<4; q++){
// menor = infinito
int menor = LLINF;
// empilha na stack auxiliar
while(!st.empty()){
int x = st.top();
menor = min(x, menor);
st.pop();
st_aux.push(x);
}
cout<<menor<<endl;
// desempilha na stack original
while(!st_aux.empty()){
int x = st_aux.top();
st_aux.pop();
st.push(x);
}
if(!st.empty()){
st.pop();
}
}
return 0;
}
Porém, é claro, a complexidade do código não é boa. ficaria aproximadamente O(Q*N), se o Q e o N forem grandes, certamente levaríamos TLE (Time Limit Exceeded).
A solução para esse problema então, seríamos usar a pilha de mínimo.
Como funciona?
A pilha de mínimo usa um valor auxiliar para armazenar o menor elemento até a inserção atual, podemos usar um stack<pair<int,int>> ou duas stack<int>.
O algoritmo então inicia a inserção de N elementos, e para cada inserção de elemento, vamos verificar se o elemento da stack auxiliar é menor ou maior que o da original, e guardaremos o de menor valor na stack auxiliar.
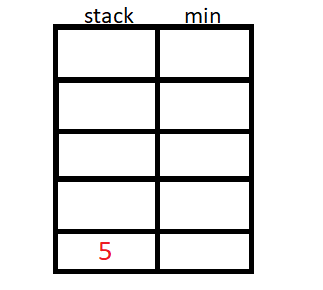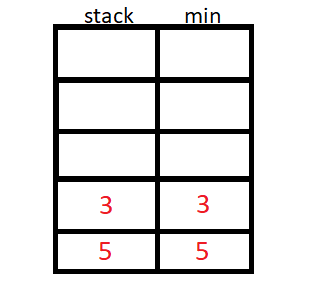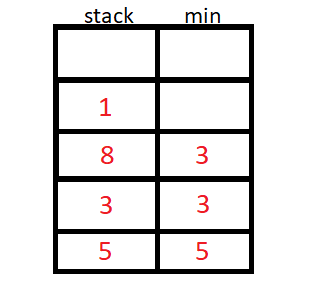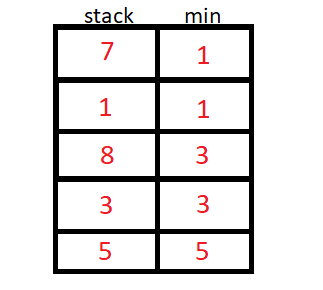
Implementação
#include <bits/stdc++.h>
using namespace std;
int main(){
stack<pair<int,int>> st;
int n; cin>>n;
// recebemos n números
for(int i=0; i<n; i++){
int num;
cin>>num;
if(st.empty()){
// num sera o menor valor da pilha.second
st.push({num,num});
}else{
// armazenamos o menor valor entre
// o que esta na pilha.second e o num atual
int menor = st.top().second;
menor = min(menor, num);
st.push({num, menor});
}
}
// Para Q consultas
int q; cin>>q;
for(int i=0; i<q; i++){
if(!st.empty()){
// pega o menor valor
int val = st.top().second;
st.pop();
cout<<val<<endl;
}
}
return 0;
}
E a complexidade fica somente O(N+Q), pois agora conseguimos responder em O(1) cada query.
Referências:
Fila
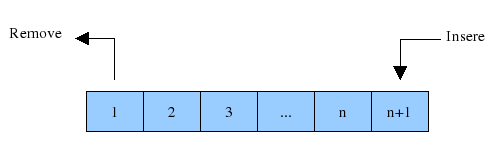
A fila segue o padrão de FIFO (first-in first-out), ao contrário da pilha, o primeiro elemento inserido será o primeiro a ser removido. Ela é muito útil para problemas que precisamos manter os elementos na ordem em que lhes foram dados.
Métodos
push- Adiciona um elemento no fim da fila.front- Retorna o elemento do início da fila.back- Retorna o elemento do final da fila.pop- Remove o elemento do início da fila.empty- Retorna true se estiver vazia, e false caso contrário.size- Retorna quantos elementos tem na fila.
Exemplo
#include <bits/stdc++.h>
using namespace std;
int main(){
queue<int> q;
q.push(9);
q.push(5);
q.push(6);
q.push(1);
q.push(8);
cout<< q.size() <<endl;
while(!q.empty()){
int elemento = q.front();
cout<<elemento<<" ";
q.pop();
}
return 0;
}
Saída
9 5 6 1 8
Fila de Prioridade
Uma fila de prioridade tem como principal característica a ordenação, ela mantém o elemento do topo como sempre sendo o maior (ou o menor) elemento sempre.
Caso esteja fixado para o elemento do topo ser o maior, a fila de prioridade estará em ordem descrescente do topo para baixo. Caso contrário, a ordem será crescente.
Por padrão, ela estará fixado para o elemento do topo ser o maior, logo, estará em ordem decrescente os elementos na fila de prioridade.
As filas de prioridades são muito úteis quando precisamos que nossos elementos sempre estejam ordenados conforme vamos inserindo elementos.
Métodos
push- Adiciona um elemento na fila de prioridade.pop- Remove o elemento do topo da fila de prioridade.top- Retorna o valor do topoempty- Retorna true se a fila estiver vazia, caso contrário, retorna falsesize- Retorna o tamanho da fila de prioridade.
A complexidade de inserção e remoção é O(log(n)), e a de olhar o topo do heap é O(1).
Exemplo
#include <bits/stdc++.h>
using namespace std;
int main(){
priority_queue<int> q;
q.push(9);
q.push(5);
q.push(6);
q.push(1);
q.push(8);
cout<< q.size() <<endl;
while(!q.empty()){
int elemento = q.top();
cout<<elemento<<" ";
q.pop();
}
return 0;
}
Saída
9 8 6 5 1
Ordenação pelo menor valor
Para ordenar pelo menor valor usamos a seguinte sintaxe na declaração:
priority_queue <int, vector<int>, greater<int>> q
Exemplo 2
#include <bits/stdc++.h>
using namespace std;
int main(){
priority_queue <int, vector<int>, greater<int>> q;
q.push(9);
q.push(5);
q.push(6);
q.push(1);
q.push(8);
cout<< q.size() <<endl;
while(!q.empty()){
int elemento = q.top();
cout<<elemento<<" ";
q.pop();
}
return 0;
}
Saída
1 5 6 8 9