Pilha
A pilha é uma estrutura que, como o nome sugere, permite inserção e remoção apenas do “topo”. Isto significa que, ao remover um elemento da pilha, o elemento a ser removido é o último que foi inserido. Também é conhecido como LIFO (last-in first-out).
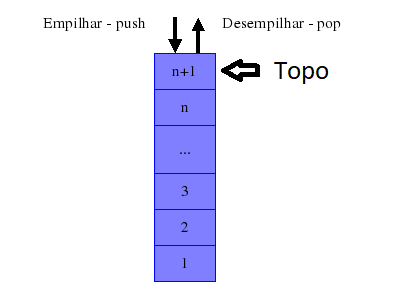
Métodos:
push- Insere um elemento na pilha.pop- Remove o elemento do topo da pilha.top- Retorna o elemento do topo da pilha.size- Retorna o tamanho da pilha.empty- Retorna true se estiver vazia, se não, retorna falso.
Exemplo
- Programa simples que vai inserir elementos na pilha e depois conforme for removendo, printa cada elemento
#include <bits/stdc++.h>
using namespace std;
int main() {
stack<int> pilha; // construtor, entre <> deve ser inserido o tipo de dado que será armazenado
pilha.push(2); // o metodo push insere o elemento no topo da pilha
pilha.push(7);
pilha.push(8);
pilha.push(4);
cout << pilha.size() << endl; // tamanho da pilha
// enquanto não estiver vazia, remove o elemento do topo e printa ele
while(!pilha.empty()){
int elemento = pilha.top();
cout<<elemento<<" ";
pilha.pop();
}
return 0;
}
Saída
4 8 7 2
Pilha de Mínimo
E se quisermos o seguinte problema:
- Dado N números em uma pilha, para os últimos Q números na pilha, printe o menor número em toda pilha até então.
Podemos fazer um código que para cada Q últimos números na pilha, podemos ir percorrendo toda a pilha restante, salvando os menores, sem alterar a pilha atual.
#include <bits/stdc++.h>
using namespace std;
int main(){
stack<int> st;
st.push(5);
st.push(3);
st.push(8);
st.push(1);
st.push(7);
stack<int> st_aux;
// para os 4 últimos números, printe o menor número de toda a pilha até ele
for(int q=0; q<4; q++){
// menor = infinito
int menor = LLINF;
// empilha na stack auxiliar
while(!st.empty()){
int x = st.top();
menor = min(x, menor);
st.pop();
st_aux.push(x);
}
cout<<menor<<endl;
// desempilha na stack original
while(!st_aux.empty()){
int x = st_aux.top();
st_aux.pop();
st.push(x);
}
if(!st.empty()){
st.pop();
}
}
return 0;
}
Porém, é claro, a complexidade do código não é boa. ficaria aproximadamente O(Q*N), se o Q e o N forem grandes, certamente levaríamos TLE (Time Limit Exceeded).
A solução para esse problema então, seríamos usar a pilha de mínimo.
Como funciona?
A pilha de mínimo usa um valor auxiliar para armazenar o menor elemento até a inserção atual, podemos usar um stack<pair<int,int>> ou duas stack<int>.
O algoritmo então inicia a inserção de N elementos, e para cada inserção de elemento, vamos verificar se o elemento da stack auxiliar é menor ou maior que o da original, e guardaremos o de menor valor na stack auxiliar.
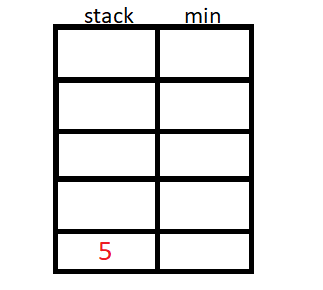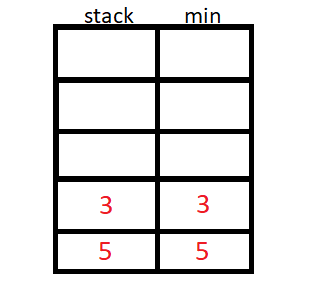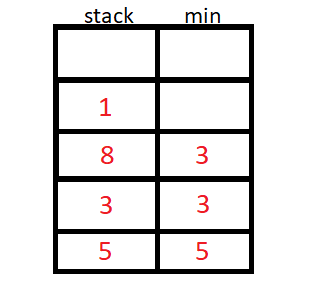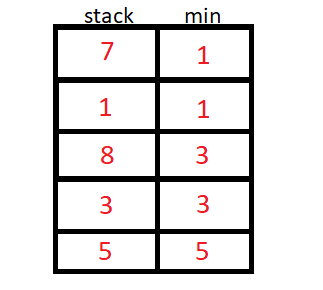
Implementação
#include <bits/stdc++.h>
using namespace std;
int main(){
stack<pair<int,int>> st;
int n; cin>>n;
// recebemos n números
for(int i=0; i<n; i++){
int num;
cin>>num;
if(st.empty()){
// num sera o menor valor da pilha.second
st.push({num,num});
}else{
// armazenamos o menor valor entre
// o que esta na pilha.second e o num atual
int menor = st.top().second;
menor = min(menor, num);
st.push({num, menor});
}
}
// Para Q consultas
int q; cin>>q;
for(int i=0; i<q; i++){
if(!st.empty()){
// pega o menor valor
int val = st.top().second;
st.pop();
cout<<val<<endl;
}
}
return 0;
}
E a complexidade fica somente O(N+Q), pois agora conseguimos responder em O(1) cada query.
Referências: