Subsecções de Fundamentos do C++
Complexidade
O que é Complexidade?
Em linhas gerais, a complexidade de tempo de um algoritmo é o quanto as variáveis de entrada impactam no seu tempo de execução.
Para se referir a complexidade de um algoritmo, se usa a notação Big O, denotada por O(N). A notação Big O tem o seguinte significado: No pior caso da execução deste algoritmo, o número de operações realizado será proporcional a N, e por simplicidade, eliminamos constantes e fatores não dominantes. A quantidade de operações que os computadores atuais executam em um segundo é por volta de 10^8, portanto podemos estimar o tempo de execução de um programa usando análise de complexidade. Basta fazer o cálculo de complexidade e dividir por 10^8, e a resposta será aproximadamente o tempo de execução em segundos. Esse mesmo conceito se extende a memória utilizada por um programa, podemos fazer o cálculo de complexidade e dividir o resultado por 10^6, e saberemos quantos MegaBytes serão utilizados pelo programa no pior caso.
Exemplos:
printf("Hello World\n");
Esse código tem complexidade O(1) (também chamado de complexidade constante), porque nenhuma variável de entrada impacta no seu tempo de execução. A complexidade de memória também é O(1).
Loops
int n;
scanf("%d",&n);
for(int i = 0; i < n; i++){
printf("%d\n",i);
}
Esse código tem complexidade O(n), pois o seu tempo tempo de execução cresce linearmente dependendo da variável n. A memória necessária não depende de nenhuma variável de entrada então é O(1).
int n;
scanf("%d",&n);
for(int i = 0; i < 10*n; i++){
printf("%d\n",i);
}
Esse código também tem complexidade O(n), porque eliminamos os fatores constantes para manter a simplicidade. Complexidade de memória O(1).
int n,m;
scanf("%d %d",&n,&m);
for(int i = 0; i < n; i++){
printf("%d\n",i);
}
for(int i = 0; i < m; i++){
printf("%d\n",i);
}
Muitas vezes, a complexidade depende de mais de uma variável de entrada. Como não temos nenhuma informação sobre o significado das variáveis, a complexidade é O(n+m). Se soubéssemos por exemplo que m fosse sempre muito maior que m, poderíamos dizer O(m). Mais uma vez a memória utilizada não depende de nenhuma variável de entrada.
Multiplicação de matrizes
O código abaixo computa C = A * B, onde A é uma matriz n por p e B é uma matriz p por m.
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
C[i][j] = 0;
for(int k = 0; k < p; k++){
C[i][j] += A[i][k] * B[k][j];
}
}
}
Como os fors estão aninhados a complexidade do código é a multiplicação das complexidades de cada for, sendo então, O(n*m*p). A multiplicação produz a matriz C como resultado, que tem dimenções n por m, Como é necessário alocar esse espaço, a complexidade de memória é O(n*m).
Ordenação
Um problema bastante estudado é o de ordenação. Existem vários algoritmos resolvem o problema eficientemente, não será mostrado um desses. O código a seguir ordena um vetor v de tamanho n.
for(int i = 0; i < n; i++){
for(int j = i; j < n; j++){
if(v[i] > v[j]){
tmp = v[i];
v[i] = v[j];
v[j] = tmp;
}
}
}
A quantidade de vezes que o segundo loop executa depende do i, então é um pouco mais difícil de analisar a complexidade.
Ao longo das iterações do primeiro loop, a quantidade de iterações do segundo é n + (n-1) + (n-2) + (n-3) + ... + 1, ou seja, é soma de PA e podemos resolver para O((n+1)*n/2). Em análise de complexidade só nos importamos com quando as variáveis são muito grandes(tendem a infinito), de um modo bem bruto infinito e infinito/2 dá no mesmo, então podemos escrever a complexidade como O((n+1)*n). Novamente quando pensamos em números bem altos n e n+1 se tornam praticamente a mesma coisa e podemos concluir que a complexidade é O(n^2).
Portanto podemos dizer que a complexidade do código acima é O((n+1)*n/2), O((n+1)*n) ou O(n^2). Mas geralmente optamos pela forma mais simples que é O(n^2).
A intuição sobre a complexidade de memória pode acabar te enganando nesse exemplo. O motivo é o seguinte: o código apenas troca os valores de lugar dentro do vetor, não sendo necessário alocar um novo vetor com a resposta(Ao contrário da multiplicação de matrizes), então a complexidade de memória é O(1).
Recursão
Também é possível analisar a complexidade de funções recursivas.
Exponenciação
int slow_exp(int base, int e){
if(e == 0)
return 1;
return base * slow_exp(base,e-1);
}
Nessa função, em cada chamada, o expoente decresce em um, atingindo o caso base quando se iguala a 0. Então são feitas O(n) chamadas. Quando avaliamos complexidade de memória de funções recursivas, temos que levar em conta a pilha de execução também. São empilhadas n chamadas na pilha, então a complexidade de memória é O(n).
Exponenciação rápida
int fast_exp(int base, int e){
if(e == 0)
return 1;
if(e % 2)
return base * fast_exp(base * base,e/2);
else
return fast_exp(base * base, e/2);
}
Essa é uma função que também computa uma exponenciação. É um bom exemplo de como problemas abordados de forma diferente ou usando propriedades matemáticas podem ser resolvidos de forma mas eficiente. Em cada chamada na recursão, o expoente é dividido por 2, atingindo o caso base quando se iguala a 0. É fácil ver que o número 2^k levaria k chamadas para atingir o caso base, isso ocorre porque log2 (2^k) = k, então a complexidade é O(log N). A complexidade de memória é justificada da mesma forma que no caso anterior, a memória utilizada será o número de chamadas recursivas, então, O(log n).
Fibonacci
int fibonacci(int n){
if(n == 0)
return 0;
if(n == 1)
return 1;
return fibonacci(n-1) + fibonacci(n-2);
}
A famosa função de fibonacci. Essa função recursiva é bem bonita de se ver declarada, mas não é nada eficiente.
Pense que queremos Calcular Fibonacci(7)
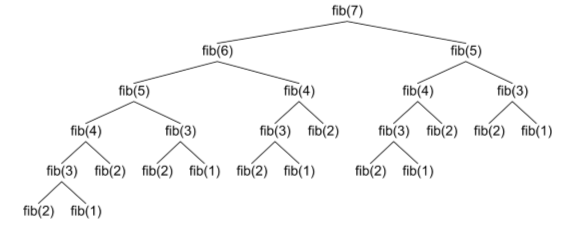
Essa a árvore formada pelas chamadas recursivas, olhe quantas vezes recomputamos as mesmas coisas. A complexidade dessa função é O(2^n), pois para cada chamada de fibonacci recursiva, fazemos outras duas, e acabamos recomputando várias vezes as mesmas coisas. Implemente essa função em sua máquina e faça uma chamada de fibonacci(40), já deve ser possível sentir o tempo que o programa leva para processar isso.
A complexidade de memória dessa função pode ser um pouco mais complicada de analisar vamos por partes. No total, serão feitos O(2^n) chamadas recursivas, e todas elas precisaram de um espaço na pilha de execução, no entanto, as 2^n chamadas não coexistirão na pilha de execução. Olhando bem atentamente e seguindo o fluxo das chamadas recursivas, é possível ver que no máximo um ‘ramo’ da árvore estará na pilha por vez, o ramo mais longo tem comprimento n portanto, complexidade de memória O(n).
VideoAulas Complementares
https://www.youtube.com/watch?v=YoZPTyGL2IQ (12 min.)
https://www.youtube.com/watch?v=moPtwq_cVH8 (51 min. MIT)
Entrada/Saída
Entrada
O objeto “cin” representa o stream de entrada no C++. Ele realiza a leitura de um sequência de dados, sem espaços e sem tabulações, vindas do teclado. Para coletar estes dados armazenados, usa-se o “operador de extração” que “extrai” dados do stream.
Lendo um Input
A primeira linha terá N que é a quantidade de números a serem lidos.
A segunda linha será os N números.
input:
4
1 5 2 3
#include <bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
for(int i=0; i<n; i++){
int numero;
cin>>numero;
}
return 0;
}
Saída
O objeto “cout” representa o stream de saída no C++. Este stream é uma espécie de sequência (fluxo) de dados a serem impressos na tela. Para realizar a impressão, usa-se o “operador de inserção” que “insere” dados dentro do stream.
Printando o famoso “Hello World”
#include <bits/stdc++.h>
using namespace std;
int main(){
cout<<"Hello World"<<endl;
return 0;
}
O “endl” é usado para fazer quebra de linha, porém, pode ser mais lento que o “\n”.
Casas Decimais
Para printar as casas decimais, precisamos usar o “fixed” que é uma função do C++ usada para formatar a saída, juntamente com o “setprecision”, que diz quantas casas será printada.
#include <bits/stdc++.h>
using namespace std;
int main(){
double pi = 3.141592653;
cout<<fixed;
cout<<setprecision(4);
cout<<pi<<endl;
// 3.1415
return 0;
}
Fast Cin
O printf e o scanf do C são mais rápidos do que o cin e o cout do C++.
Isso ocorre porque o C++ usa a sincronização do output, ou seja, enquanto ele está lendo o input, o programa pode responder ao mesmo tempo.
A resolução para que o cin e o cout fique mais rápido (próximo à velocidade do scanf e do printf), é desabilitar a sincronização no C++.
Segue o exemplo:
ios_base::sync_with_stdio(false);
cin.tie(NULL);
Exemplo
#include <bits/stdc++.h>
using namespace std;
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
return 0;
}
Declarações
Subpáginas
Subsecções de Declarações
Strings
No C++ representa uma sequência de caracteres
Podemos declarar uma string como:
string nomevar;
string nomevar = constante;
string nomevar = char ∗ variavel;
string nomevar(char ∗ variavel);
string nomevar(tamanho, constante char);
Concatenação
Podemos usar o operador “+” para concatenar duas strings
#include <bits/stdc++.h>
using namespace std;
int main(){
string a = "abc";
string b = "def";
string c = a + b;
cout<<c<<endl;
// abcdef
return 0;
}
Transformando um inteiro em string
Podemos transformar um inteiro em uma string usando a função “to_string()”
#include <bits/stdc++.h>
using namespace std;
int main(){
int x = 123;
string s = to_string(x);
cout<<s<<endl;
return 0;
}
Vector
Vector pode ser entendido como uma estruturas de dados similar a um array de tamanho expansível.
A diferença principal entre vector e array é a alocação: no array adota-se alocação estática, enquanto que no vector a alocaçãao é dinâmica.
Inicializar
#include <bits/stdc++.h>
using namespace std;
int main(){
// inicializando vetores vazios
vector<double> vd;
vector<pair<int,double>> vid;
vector<string> vs;
vector<int> v;
// vector<int> v(tamanho, valor)
vector<int> v(4, 0); // {0, 0, 0, 0} vetor de 4 posições com valor 0
vector<int> v(4); // {0, 0, 0, 0} por default, inicializa como 0
v.push_back(5); // Adiciona o elemento 5
// v = {0, 0, 0, 0, 5}
v.pop_back();
// v = {0, 0, 0, 0}
}
Iterar
#include <bits/stdc++.h>
using namespace std;
int main(){
vector<int> v = {1, 2, 3, 4, 5};
// printa um elemento em cada linha
for(int i=0; i<v.size(); i++){
cout<< v[i] << endl;
}
}
O método size() retorna a quantidade de elementos existentes em um vector. Complexidade: O(1)
Ordenar
O(N*log(N))
#include <bits/stdc++.h>
using namespace std;
int main(){
vector<int> v = {3, 4, 1, 2, 5};
sort(v.begin(), v.end()); // ordena o vetor
// v = {1, 2, 3, 4, 5}
}
Inverter
O(N)
#include <bits/stdc++.h>
using namespace std;
int main(){
vector<int> v = {1, 2, 3, 4, 5};
reverse(v.begin(), v.end());
// v = {5, 4, 3, 2, 1}
}
Vector de Pair
#include <bits/stdc++.h>
using namespace std;
int main(){
vector<pair<int,int>> v = {{1, 2}, {3, 4}, {5, 6}};
// v[0].first = 1
// v[0].second = 2
}
Pairs
O pair é muito importante quando precisamos guardar duas informações juntas.
Um “pair” é um contêiner que consiste de dois tipos de dados ou objetos.
Declaramos um pair como:
pair<tipodado1, tipodado2> variavel;
Podemos inicializá-lo usando o make_pair ou diretamente:
variavel = make_pair(dado1, dado2);
variavel = {dado1, dado2};
- O primeiro elemento é acessado usando o “first” e o segundo usando “second”
variavel.first;
variavel.second;
Exemplo 1:
- Um Pair que armazena 2 inteiros
#include <bits/stdc++.h>
using namespace std;
int main(){
pair<int, int> pii;
pii = {5, 10};
cout<< pii.first << " " << pii.second<<"\n";
// 5 10
return 0;
}
Exemplo 2:
- Um Pair que armazena 1 inteiro e 1 double
#include <bits/stdc++.h>
using namespace std;
int main(){
pair<int, double> pii;
pii = {2, 1.5365};
cout<< pii.first << " " << pii.second<<"\n";
// 2 1.5365
return 0;
}
Comparando Variáveis:
#include <bits/stdc++.h>
using namespace std;
int main(){
pair<int, int> v1, v2;
v1 = {3, 1};
v2 = {2, 2};
if(v1 > v2) cout<< "v1 é maior que v2";
else cout<< "v1 é menor ou igual a v2";
return 0;
}
Iterators
Iterators são tipos específicos de ponteiros que referenciam endereçoos de memória de objetos e contêiners STL.
Exemplo 1
#include <bits/stdc++.h>
using namespace std;
int main(){
vector<int> v = {1, 2, 3, 4, 5};
vector<int>::iterator ptr;
cout<<"Elementos do Vetor"<<endl;
for(ptr = v.begin(); ptr != v.end(); ptr++){
cout<<(*ptr)<<endl;
}
return 0;
}
Você pode usar o auto no lugar de vector<int>::iterator, para facilitar
Exemplo 2
#include <bits/stdc++.h>
using namespace std;
int main(){
vector<int> ar = { 1, 2, 3, 4, 5 };
// Declaring iterators to a vector
vector<int>::iterator ptr = ar.begin();
vector<int>::iterator ftr = ar.end();
// Using next() to return new iterator
// points to 4
auto it = next(ptr, 3);
// Using prev() to return new iterator
// points to 3
auto it1 = prev(ftr, 3);
// Displaying iterator position
cout << "The position of new iterator using next() is : ";
cout << *it << " ";
cout << endl;
// Displaying iterator position
cout << "The position of new iterator using prev() is : ";
cout << *it1 << " ";
cout << endl;
// The position of new iterator using next() is : 4
// The position of new iterator using prev() is : 3
}
Estrutura de Dados
Subpáginas
Subsecções de Estrutura de Dados
ED Linear
Subpáginas
Subsecções de ED Linear
Pilha
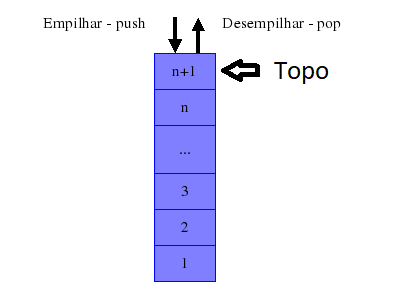
A pilha é uma estrutura que, como o nome sugere, permite inserção e remoção apenas do “topo”. Isto significa que, ao remover um elemento da pilha, o elemento a ser removido é o último que foi inserido. Também é conhecido como LIFO (last-in first-out).
Métodos:
push- Insere um elemento na pilha.pop- Remove o elemento do topo da pilha.top- Retorna o elemento do topo da pilha.size- Retorna o tamanho da pilha.empty- Retorna true se estiver vazia, se não, retorna falso.
Exemplo
- Programa simples que vai inserir elementos na pilha e depois conforme for removendo, printa cada elemento
#include <bits/stdc++.h>
using namespace std;
int main() {
stack<int> pilha; // construtor, entre <> deve ser inserido o tipo de dado que será armazenado
pilha.push(2); // o metodo push insere o elemento no topo da pilha
pilha.push(7);
pilha.push(8);
pilha.push(4);
cout << pilha.size() << endl; // tamanho da pilha
// enquanto não estiver vazia, remove o elemento do topo e printa ele
while(!pilha.empty()){
int elemento = pilha.top();
cout<<elemento<<" ";
pilha.pop();
}
return 0;
}
Saída
4 8 7 2
Pilha de Mínimo
E se quisermos o seguinte problema:
- Dado N números em uma pilha, para os últimos Q números na pilha, printe o menor número em toda pilha até então.
Podemos fazer um código que para cada Q últimos números na pilha, podemos ir percorrendo toda a pilha restante, salvando os menores, sem alterar a pilha atual.
#include <bits/stdc++.h>
using namespace std;
int main(){
stack<int> st;
st.push(5);
st.push(3);
st.push(8);
st.push(1);
st.push(7);
stack<int> st_aux;
// para os 4 últimos números, printe o menor número de toda a pilha até ele
for(int q=0; q<4; q++){
// menor = infinito
int menor = LLINF;
// empilha na stack auxiliar
while(!st.empty()){
int x = st.top();
menor = min(x, menor);
st.pop();
st_aux.push(x);
}
cout<<menor<<endl;
// desempilha na stack original
while(!st_aux.empty()){
int x = st_aux.top();
st_aux.pop();
st.push(x);
}
if(!st.empty()){
st.pop();
}
}
return 0;
}
Porém, é claro, a complexidade do código não é boa. ficaria aproximadamente O(Q*N), se o Q e o N forem grandes, certamente levaríamos TLE (Time Limit Exceeded).
A solução para esse problema então, seríamos usar a pilha de mínimo.
Como funciona?
A pilha de mínimo usa um valor auxiliar para armazenar o menor elemento até a inserção atual, podemos usar um stack<pair<int,int>> ou duas stack<int>.
O algoritmo então inicia a inserção de N elementos, e para cada inserção de elemento, vamos verificar se o elemento da stack auxiliar é menor ou maior que o da original, e guardaremos o de menor valor na stack auxiliar.
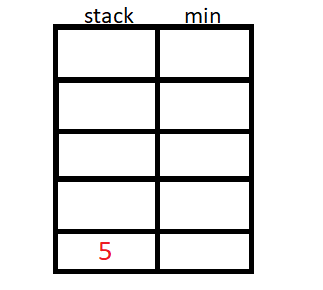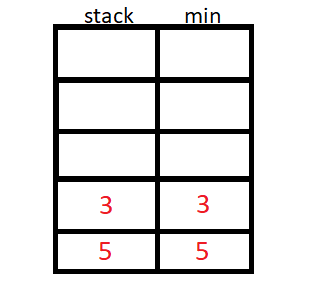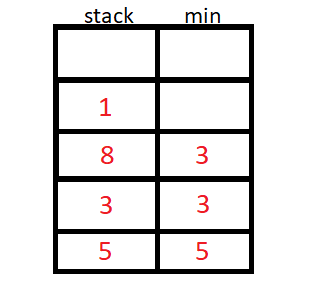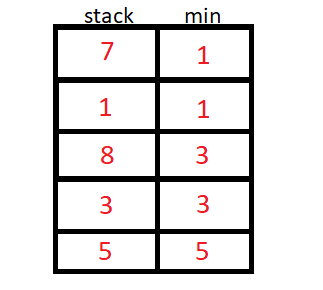
Implementação
#include <bits/stdc++.h>
using namespace std;
int main(){
stack<pair<int,int>> st;
int n; cin>>n;
// recebemos n números
for(int i=0; i<n; i++){
int num;
cin>>num;
if(st.empty()){
// num sera o menor valor da pilha.second
st.push({num,num});
}else{
// armazenamos o menor valor entre
// o que esta na pilha.second e o num atual
int menor = st.top().second;
menor = min(menor, num);
st.push({num, menor});
}
}
// Para Q consultas
int q; cin>>q;
for(int i=0; i<q; i++){
if(!st.empty()){
// pega o menor valor
int val = st.top().second;
st.pop();
cout<<val<<endl;
}
}
return 0;
}
E a complexidade fica somente O(N+Q), pois agora conseguimos responder em O(1) cada query.
Referências:
Fila
A fila segue o padrão de FIFO (first-in first-out), ao contrário da pilha, o primeiro elemento inserido será o primeiro a ser removido. Ela é muito útil para problemas que precisamos manter os elementos na ordem em que lhes foram dados.
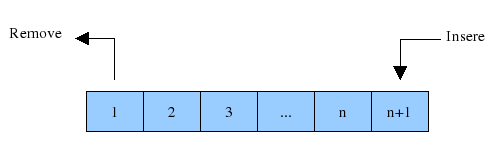
Métodos
push- Adiciona um elemento no fim da fila.front- Retorna o elemento do início da fila.back- Retorna o elemento do final da fila.pop- Remove o elemento do início da fila.empty- Retorna true se estiver vazia, e false caso contrário.size- Retorna quantos elementos tem na fila.
Exemplo
#include <bits/stdc++.h>
using namespace std;
int main(){
queue<int> q;
q.push(9);
q.push(5);
q.push(6);
q.push(1);
q.push(8);
cout<< q.size() <<endl;
while(!q.empty()){
int elemento = q.front();
cout<<elemento<<" ";
q.pop();
}
return 0;
}
Saída
9 5 6 1 8
Fila de Prioridade
Uma fila de prioridade tem como principal característica a ordenação, ela mantém o elemento do topo como sempre sendo o maior (ou o menor) elemento sempre.
Caso esteja fixado para o elemento do topo ser o maior, a fila de prioridade estará em ordem descrescente do topo para baixo. Caso contrário, a ordem será crescente.
Por padrão, ela estará fixado para o elemento do topo ser o maior, logo, estará em ordem decrescente os elementos na fila de prioridade.
As filas de prioridades são muito úteis quando precisamos que nossos elementos sempre estejam ordenados conforme vamos inserindo elementos.
Métodos
push- Adiciona um elemento na fila de prioridade.pop- Remove o elemento do topo da fila de prioridade.top- Retorna o valor do topoempty- Retorna true se a fila estiver vazia, caso contrário, retorna falsesize- Retorna o tamanho da fila de prioridade.
A complexidade de inserção e remoção é O(log(n)), e a de olhar o topo do heap é O(1).
Exemplo
#include <bits/stdc++.h>
using namespace std;
int main(){
priority_queue<int> q;
q.push(9);
q.push(5);
q.push(6);
q.push(1);
q.push(8);
cout<< q.size() <<endl;
while(!q.empty()){
int elemento = q.top();
cout<<elemento<<" ";
q.pop();
}
return 0;
}
Saída
9 8 6 5 1
Ordenação pelo menor valor
Para ordenar pelo menor valor usamos a seguinte sintaxe na declaração:
priority_queue <int, vector<int>, greater<int>> q
Exemplo 2
#include <bits/stdc++.h>
using namespace std;
int main(){
priority_queue <int, vector<int>, greater<int>> q;
q.push(9);
q.push(5);
q.push(6);
q.push(1);
q.push(8);
cout<< q.size() <<endl;
while(!q.empty()){
int elemento = q.top();
cout<<elemento<<" ";
q.pop();
}
return 0;
}
Saída
1 5 6 8 9
ED Não Linear
Subpáginas
Subsecções de ED Não Linear
Map
O map é uma estrutura interessante pois permite “mapear” chaves à valores, e dado uma chave encontrar o seu valor rapidamente (complexidade depende da implementação). Por exemplo, podemos fazer um map com strings de chave e int de valor, sendo possível recuperar o valor inteiro associado a aquela string rapidamente.
Deve-se ter cuidado com o uso de map pois ele é implementado em c++ como um set de pairs, isto é, vai ter complexidade O(log n) para inserir e modificar dados.
Existe também o unordered_map, que é uma estrutura que usa hash. No pior caso é linear, mas em média tem complexidade constante. O seu funcionamento é similar ao do map, com a diferença de que seus elementos não estão ordenados.
Métodos
insert({key, element})- Insere uma chave e um valor no maperase()- Remove uma key ou um iteratorfind(element)- Retorna um iterator da posição do elementcount- Retorna a quantidade de elementos de uma chave específicasize- Retorna o tamanho do mapclear- Limpa todo o conteúdo do Mapbegin- Retorna um iterator para o início do mapend- Retorna um iterator para o final do map
Inicialização
#include <bits/stdc++.h>
using namespace std;
int main(){
// map chave, valor de inteiros
map<int, int> m; // Inicialização de map vazio
map<int, int> m = {{2, 3}, {4, 6}}; // Inicialização de map com valor
m[7] = 3
m[7] ++; // 4
}
Iteração
#include <bits/stdc++.h>
using namespace std;
int main(){
// iterando por métodos iterator
map<int, int> m = {{2, 3}, {4, 6}};
// Printa a chave e o valor em cada linha
for(auto it = m.begin(); it != m.end(); it++){
cout<< it.first <<" "<< it.second<< endl;
}
// tambem pode ser escrito como:
for(auto it: m){
cout<< it.first << " "<< it.second<< endl;
}
}
Saída
2 3
4 6
Apagando elemento
#include <bits/stdc++.h>
using namespace std;
int main(){
// iterando por métodos iterator
map<int, int> m = {{2, 3}, {4, 6}}
m.erase(m.find(2));
m.erase(4);
}
Da primeira maneira, ele apaga em tempo constante, pois está passando um iterator. Da segunda maneira, ele apaga em log(N), pois ele faz uma busca no elemento.
Verificar um elemento
#include <bits/stdc++.h>
using namespace std;
int main(){
// iterando por métodos iterator
map<int, int> m = {{2, 3}, {4, 6}}
if( m.count(2) > 0 ){ // existe uma chave {2}
cout<< "Elemento existe";
}else{
cout<< "Elemento não existe";
}
}
Saída
Elemento existe
Set
A estrutura set é bem parecida com o que conhecemos de conjuntos da matemática; não existem elementos repetidos e a ordem não importa.
A implementação do set, porém, é feita com uma árvore binária de busca, sendo assim permitido inserir, remover e acessar um elemento em O(log n).
A vantagem do set em relação ao vector é que, caso queira inserir um elemento em um vector ordenado e preservar a ordenação, você terá que procurar o lugar que ele deve ser inserido, fazer a inserção e modificar a posição dos elementos à direita dele. Modificar todas as posições à direita tem uma complexidade ruim O(n), então este algoritmo será mais eficiente com o set.
Além da vantagem de eficiência, essas operações com set são feitas com alguns simples métodos!
Métodos
insert(element)- Insere um elemento no Seterase()- Remove uma key ou um iteratorfind(element)- Retorna um iterator da posição do elementcount- Retorna a quantidade de elementos de uma chave específicasize- Retorna o tamanho do setclear- Limpa todo o conteúdo do setbegin- Retorna um iterator para o início do setend- Retorna um iterator para o final do setlower_bound(element)- Retorna um iterator para o primeiro valor >= elementupper_bound(element)- Retorna um iterator para o primeiro valor > element
Exemplo 1
#include <bits/stdc++.h>
using namespace std;
int main() {
set<int> s;
s.insert(3); // insere elemento no set
cout << s.size() << endl; // tamanho do set
// para verificar se um elemento está contido no set ou nao podemos utilizar
// o metodo find; caso nao esteja presente ele retornará o iterator para
// o fim do set
if(s.find(2) == s.end()) {
cout << "O numero 2 nao esta no set" << endl;
}
else {
cout << "O numero 2 esta no set" << endl;
}
if(s.find(3) == s.end()) {
cout << "O numero 3 nao esta no set" << endl;
}
else {
cout << "O numero 3 esta no set" << endl;
}
s.erase(3); // apaga elemento 3 do set
if(s.find(3) == s.end()) {
cout << "O numero 3 nao esta no set" << endl;
}
else {
cout << "O numero 3 esta no set" << endl;
}
return 0;
}
Outro método extremamente útil é o lower_bound (e o upper_bound). O lower_bound recebe um inteiro x como argumento e retorna o menor inteiro maior ou igual a x. Caso não exista, ele retorna um iterator para o fim do set (set.end()).
Exemplo 2
#include <bits/stdc++.h>
using namespace std;
int main() {
set<int> s;
s.insert(3); // insere elemento no set
s.insert(4);
s.insert(5);
s.insert(7);
auto iterator1 = s.lower_bound(6);
// se iterator eh igual a s.end() entao nao existe
if(iterator1 != s.end()) {
int numero = *iterator1;
cout << "menor inteiro maior ou igual a 6 eh " << numero << endl;
}
else {
cout << "nao existe inteiro numero maior ou igual a 6" << endl;
}
auto iterator2 = s.lower_bound(9);
// se iterator eh igual a s.end() entao nao existe
if(iterator2 != s.end()) {
int numero = *iterator2;
cout << "menor inteiro maior ou igual a 9 eh " << numero << endl;
}
else {
cout << "nao existe inteiro numero maior ou igual a 9" << endl;
}
return 0;
}
Na verdade, você pode utilizar o lower_bound para qualquer tipo que implemente a operação “<”, como por exemplo o pair<int, int>.