Subsecções de Materiais
Fundamentos do C++
Tudo o que você precisa saber sobre C++
Subpáginas
Subsecções de Fundamentos do C++
Complexidade
O que é Complexidade?
Em linhas gerais, a complexidade de tempo de um algoritmo é o quanto as variáveis de entrada impactam no seu tempo de execução.
Para se referir a complexidade de um algoritmo, se usa a notação Big O, denotada por O(N). A notação Big O tem o seguinte significado: No pior caso da execução deste algoritmo, o número de operações realizado será proporcional a N, e por simplicidade, eliminamos constantes e fatores não dominantes. A quantidade de operações que os computadores atuais executam em um segundo é por volta de 10^8, portanto podemos estimar o tempo de execução de um programa usando análise de complexidade. Basta fazer o cálculo de complexidade e dividir por 10^8, e a resposta será aproximadamente o tempo de execução em segundos. Esse mesmo conceito se extende a memória utilizada por um programa, podemos fazer o cálculo de complexidade e dividir o resultado por 10^6, e saberemos quantos MegaBytes serão utilizados pelo programa no pior caso.
Exemplos:
printf("Hello World\n");
Esse código tem complexidade O(1) (também chamado de complexidade constante), porque nenhuma variável de entrada impacta no seu tempo de execução. A complexidade de memória também é O(1).
Loops
int n;
scanf("%d",&n);
for(int i = 0; i < n; i++){
printf("%d\n",i);
}
Esse código tem complexidade O(n), pois o seu tempo tempo de execução cresce linearmente dependendo da variável n. A memória necessária não depende de nenhuma variável de entrada então é O(1).
int n;
scanf("%d",&n);
for(int i = 0; i < 10*n; i++){
printf("%d\n",i);
}
Esse código também tem complexidade O(n), porque eliminamos os fatores constantes para manter a simplicidade. Complexidade de memória O(1).
int n,m;
scanf("%d %d",&n,&m);
for(int i = 0; i < n; i++){
printf("%d\n",i);
}
for(int i = 0; i < m; i++){
printf("%d\n",i);
}
Muitas vezes, a complexidade depende de mais de uma variável de entrada. Como não temos nenhuma informação sobre o significado das variáveis, a complexidade é O(n+m). Se soubéssemos por exemplo que m fosse sempre muito maior que m, poderíamos dizer O(m). Mais uma vez a memória utilizada não depende de nenhuma variável de entrada.
Multiplicação de matrizes
O código abaixo computa C = A * B, onde A é uma matriz n por p e B é uma matriz p por m.
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
C[i][j] = 0;
for(int k = 0; k < p; k++){
C[i][j] += A[i][k] * B[k][j];
}
}
}
Como os fors estão aninhados a complexidade do código é a multiplicação das complexidades de cada for, sendo então, O(n*m*p). A multiplicação produz a matriz C como resultado, que tem dimenções n por m, Como é necessário alocar esse espaço, a complexidade de memória é O(n*m).
Ordenação
Um problema bastante estudado é o de ordenação. Existem vários algoritmos resolvem o problema eficientemente, não será mostrado um desses. O código a seguir ordena um vetor v de tamanho n.
for(int i = 0; i < n; i++){
for(int j = i; j < n; j++){
if(v[i] > v[j]){
tmp = v[i];
v[i] = v[j];
v[j] = tmp;
}
}
}
A quantidade de vezes que o segundo loop executa depende do i, então é um pouco mais difícil de analisar a complexidade.
Ao longo das iterações do primeiro loop, a quantidade de iterações do segundo é n + (n-1) + (n-2) + (n-3) + ... + 1, ou seja, é soma de PA e podemos resolver para O((n+1)*n/2). Em análise de complexidade só nos importamos com quando as variáveis são muito grandes(tendem a infinito), de um modo bem bruto infinito e infinito/2 dá no mesmo, então podemos escrever a complexidade como O((n+1)*n). Novamente quando pensamos em números bem altos n e n+1 se tornam praticamente a mesma coisa e podemos concluir que a complexidade é O(n^2).
Portanto podemos dizer que a complexidade do código acima é O((n+1)*n/2), O((n+1)*n) ou O(n^2). Mas geralmente optamos pela forma mais simples que é O(n^2).
A intuição sobre a complexidade de memória pode acabar te enganando nesse exemplo. O motivo é o seguinte: o código apenas troca os valores de lugar dentro do vetor, não sendo necessário alocar um novo vetor com a resposta(Ao contrário da multiplicação de matrizes), então a complexidade de memória é O(1).
Recursão
Também é possível analisar a complexidade de funções recursivas.
Exponenciação
int slow_exp(int base, int e){
if(e == 0)
return 1;
return base * slow_exp(base,e-1);
}
Nessa função, em cada chamada, o expoente decresce em um, atingindo o caso base quando se iguala a 0. Então são feitas O(n) chamadas. Quando avaliamos complexidade de memória de funções recursivas, temos que levar em conta a pilha de execução também. São empilhadas n chamadas na pilha, então a complexidade de memória é O(n).
Exponenciação rápida
int fast_exp(int base, int e){
if(e == 0)
return 1;
if(e % 2)
return base * fast_exp(base * base,e/2);
else
return fast_exp(base * base, e/2);
}
Essa é uma função que também computa uma exponenciação. É um bom exemplo de como problemas abordados de forma diferente ou usando propriedades matemáticas podem ser resolvidos de forma mas eficiente. Em cada chamada na recursão, o expoente é dividido por 2, atingindo o caso base quando se iguala a 0. É fácil ver que o número 2^k levaria k chamadas para atingir o caso base, isso ocorre porque log2 (2^k) = k, então a complexidade é O(log N). A complexidade de memória é justificada da mesma forma que no caso anterior, a memória utilizada será o número de chamadas recursivas, então, O(log n).
Fibonacci
int fibonacci(int n){
if(n == 0)
return 0;
if(n == 1)
return 1;
return fibonacci(n-1) + fibonacci(n-2);
}
A famosa função de fibonacci. Essa função recursiva é bem bonita de se ver declarada, mas não é nada eficiente.
Pense que queremos Calcular Fibonacci(7)
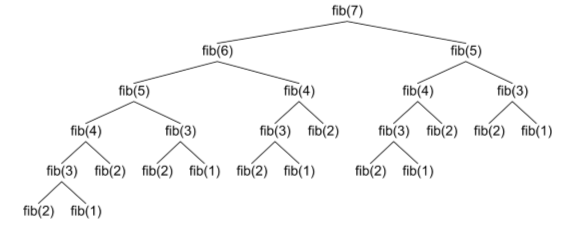
Essa a árvore formada pelas chamadas recursivas, olhe quantas vezes recomputamos as mesmas coisas. A complexidade dessa função é O(2^n), pois para cada chamada de fibonacci recursiva, fazemos outras duas, e acabamos recomputando várias vezes as mesmas coisas. Implemente essa função em sua máquina e faça uma chamada de fibonacci(40), já deve ser possível sentir o tempo que o programa leva para processar isso.
A complexidade de memória dessa função pode ser um pouco mais complicada de analisar vamos por partes. No total, serão feitos O(2^n) chamadas recursivas, e todas elas precisaram de um espaço na pilha de execução, no entanto, as 2^n chamadas não coexistirão na pilha de execução. Olhando bem atentamente e seguindo o fluxo das chamadas recursivas, é possível ver que no máximo um ‘ramo’ da árvore estará na pilha por vez, o ramo mais longo tem comprimento n portanto, complexidade de memória O(n).
VideoAulas Complementares
https://www.youtube.com/watch?v=YoZPTyGL2IQ (12 min.)
https://www.youtube.com/watch?v=moPtwq_cVH8 (51 min. MIT)
Entrada/Saída
Entrada
O objeto “cin” representa o stream de entrada no C++. Ele realiza a leitura de um sequência de dados, sem espaços e sem tabulações, vindas do teclado. Para coletar estes dados armazenados, usa-se o “operador de extração” que “extrai” dados do stream.
Lendo um Input
A primeira linha terá N que é a quantidade de números a serem lidos.
A segunda linha será os N números.
input:
4
1 5 2 3
#include <bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
for(int i=0; i<n; i++){
int numero;
cin>>numero;
}
return 0;
}
Saída
O objeto “cout” representa o stream de saída no C++. Este stream é uma espécie de sequência (fluxo) de dados a serem impressos na tela. Para realizar a impressão, usa-se o “operador de inserção” que “insere” dados dentro do stream.
Printando o famoso “Hello World”
#include <bits/stdc++.h>
using namespace std;
int main(){
cout<<"Hello World"<<endl;
return 0;
}
O “endl” é usado para fazer quebra de linha, porém, pode ser mais lento que o “\n”.
Casas Decimais
Para printar as casas decimais, precisamos usar o “fixed” que é uma função do C++ usada para formatar a saída, juntamente com o “setprecision”, que diz quantas casas será printada.
#include <bits/stdc++.h>
using namespace std;
int main(){
double pi = 3.141592653;
cout<<fixed;
cout<<setprecision(4);
cout<<pi<<endl;
// 3.1415
return 0;
}
Fast Cin
O printf e o scanf do C são mais rápidos do que o cin e o cout do C++.
Isso ocorre porque o C++ usa a sincronização do output, ou seja, enquanto ele está lendo o input, o programa pode responder ao mesmo tempo.
A resolução para que o cin e o cout fique mais rápido (próximo à velocidade do scanf e do printf), é desabilitar a sincronização no C++.
Segue o exemplo:
ios_base::sync_with_stdio(false);
cin.tie(NULL);
Exemplo
#include <bits/stdc++.h>
using namespace std;
int main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
return 0;
}
Declarações
Subpáginas
Subsecções de Declarações
Strings
No C++ representa uma sequência de caracteres
Podemos declarar uma string como:
string nomevar;
string nomevar = constante;
string nomevar = char ∗ variavel;
string nomevar(char ∗ variavel);
string nomevar(tamanho, constante char);
Concatenação
Podemos usar o operador “+” para concatenar duas strings
#include <bits/stdc++.h>
using namespace std;
int main(){
string a = "abc";
string b = "def";
string c = a + b;
cout<<c<<endl;
// abcdef
return 0;
}
Transformando um inteiro em string
Podemos transformar um inteiro em uma string usando a função “to_string()”
#include <bits/stdc++.h>
using namespace std;
int main(){
int x = 123;
string s = to_string(x);
cout<<s<<endl;
return 0;
}
Vector
Vector pode ser entendido como uma estruturas de dados similar a um array de tamanho expansível.
A diferença principal entre vector e array é a alocação: no array adota-se alocação estática, enquanto que no vector a alocaçãao é dinâmica.
Inicializar
#include <bits/stdc++.h>
using namespace std;
int main(){
// inicializando vetores vazios
vector<double> vd;
vector<pair<int,double>> vid;
vector<string> vs;
vector<int> v;
// vector<int> v(tamanho, valor)
vector<int> v(4, 0); // {0, 0, 0, 0} vetor de 4 posições com valor 0
vector<int> v(4); // {0, 0, 0, 0} por default, inicializa como 0
v.push_back(5); // Adiciona o elemento 5
// v = {0, 0, 0, 0, 5}
v.pop_back();
// v = {0, 0, 0, 0}
}
Iterar
#include <bits/stdc++.h>
using namespace std;
int main(){
vector<int> v = {1, 2, 3, 4, 5};
// printa um elemento em cada linha
for(int i=0; i<v.size(); i++){
cout<< v[i] << endl;
}
}
O método size() retorna a quantidade de elementos existentes em um vector. Complexidade: O(1)
Ordenar
O(N*log(N))
#include <bits/stdc++.h>
using namespace std;
int main(){
vector<int> v = {3, 4, 1, 2, 5};
sort(v.begin(), v.end()); // ordena o vetor
// v = {1, 2, 3, 4, 5}
}
Inverter
O(N)
#include <bits/stdc++.h>
using namespace std;
int main(){
vector<int> v = {1, 2, 3, 4, 5};
reverse(v.begin(), v.end());
// v = {5, 4, 3, 2, 1}
}
Vector de Pair
#include <bits/stdc++.h>
using namespace std;
int main(){
vector<pair<int,int>> v = {{1, 2}, {3, 4}, {5, 6}};
// v[0].first = 1
// v[0].second = 2
}
Pairs
O pair é muito importante quando precisamos guardar duas informações juntas.
Um “pair” é um contêiner que consiste de dois tipos de dados ou objetos.
Declaramos um pair como:
pair<tipodado1, tipodado2> variavel;
Podemos inicializá-lo usando o make_pair ou diretamente:
variavel = make_pair(dado1, dado2);
variavel = {dado1, dado2};
- O primeiro elemento é acessado usando o “first” e o segundo usando “second”
variavel.first;
variavel.second;
Exemplo 1:
- Um Pair que armazena 2 inteiros
#include <bits/stdc++.h>
using namespace std;
int main(){
pair<int, int> pii;
pii = {5, 10};
cout<< pii.first << " " << pii.second<<"\n";
// 5 10
return 0;
}
Exemplo 2:
- Um Pair que armazena 1 inteiro e 1 double
#include <bits/stdc++.h>
using namespace std;
int main(){
pair<int, double> pii;
pii = {2, 1.5365};
cout<< pii.first << " " << pii.second<<"\n";
// 2 1.5365
return 0;
}
Comparando Variáveis:
#include <bits/stdc++.h>
using namespace std;
int main(){
pair<int, int> v1, v2;
v1 = {3, 1};
v2 = {2, 2};
if(v1 > v2) cout<< "v1 é maior que v2";
else cout<< "v1 é menor ou igual a v2";
return 0;
}
Iterators
Iterators são tipos específicos de ponteiros que referenciam endereçoos de memória de objetos e contêiners STL.
Exemplo 1
#include <bits/stdc++.h>
using namespace std;
int main(){
vector<int> v = {1, 2, 3, 4, 5};
vector<int>::iterator ptr;
cout<<"Elementos do Vetor"<<endl;
for(ptr = v.begin(); ptr != v.end(); ptr++){
cout<<(*ptr)<<endl;
}
return 0;
}
Você pode usar o auto no lugar de vector<int>::iterator, para facilitar
Exemplo 2
#include <bits/stdc++.h>
using namespace std;
int main(){
vector<int> ar = { 1, 2, 3, 4, 5 };
// Declaring iterators to a vector
vector<int>::iterator ptr = ar.begin();
vector<int>::iterator ftr = ar.end();
// Using next() to return new iterator
// points to 4
auto it = next(ptr, 3);
// Using prev() to return new iterator
// points to 3
auto it1 = prev(ftr, 3);
// Displaying iterator position
cout << "The position of new iterator using next() is : ";
cout << *it << " ";
cout << endl;
// Displaying iterator position
cout << "The position of new iterator using prev() is : ";
cout << *it1 << " ";
cout << endl;
// The position of new iterator using next() is : 4
// The position of new iterator using prev() is : 3
}
Estrutura de Dados
Subpáginas
Subsecções de Estrutura de Dados
ED Linear
Subpáginas
Subsecções de ED Linear
Pilha
A pilha é uma estrutura que, como o nome sugere, permite inserção e remoção apenas do “topo”. Isto significa que, ao remover um elemento da pilha, o elemento a ser removido é o último que foi inserido. Também é conhecido como LIFO (last-in first-out).
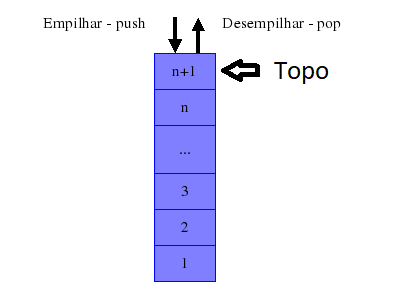
Métodos:
push- Insere um elemento na pilha.pop- Remove o elemento do topo da pilha.top- Retorna o elemento do topo da pilha.size- Retorna o tamanho da pilha.empty- Retorna true se estiver vazia, se não, retorna falso.
Exemplo
- Programa simples que vai inserir elementos na pilha e depois conforme for removendo, printa cada elemento
#include <bits/stdc++.h>
using namespace std;
int main() {
stack<int> pilha; // construtor, entre <> deve ser inserido o tipo de dado que será armazenado
pilha.push(2); // o metodo push insere o elemento no topo da pilha
pilha.push(7);
pilha.push(8);
pilha.push(4);
cout << pilha.size() << endl; // tamanho da pilha
// enquanto não estiver vazia, remove o elemento do topo e printa ele
while(!pilha.empty()){
int elemento = pilha.top();
cout<<elemento<<" ";
pilha.pop();
}
return 0;
}
Saída
4 8 7 2
Pilha de Mínimo
E se quisermos o seguinte problema:
- Dado N números em uma pilha, para os últimos Q números na pilha, printe o menor número em toda pilha até então.
Podemos fazer um código que para cada Q últimos números na pilha, podemos ir percorrendo toda a pilha restante, salvando os menores, sem alterar a pilha atual.
#include <bits/stdc++.h>
using namespace std;
int main(){
stack<int> st;
st.push(5);
st.push(3);
st.push(8);
st.push(1);
st.push(7);
stack<int> st_aux;
// para os 4 últimos números, printe o menor número de toda a pilha até ele
for(int q=0; q<4; q++){
// menor = infinito
int menor = LLINF;
// empilha na stack auxiliar
while(!st.empty()){
int x = st.top();
menor = min(x, menor);
st.pop();
st_aux.push(x);
}
cout<<menor<<endl;
// desempilha na stack original
while(!st_aux.empty()){
int x = st_aux.top();
st_aux.pop();
st.push(x);
}
if(!st.empty()){
st.pop();
}
}
return 0;
}
Porém, é claro, a complexidade do código não é boa. ficaria aproximadamente O(Q*N), se o Q e o N forem grandes, certamente levaríamos TLE (Time Limit Exceeded).
A solução para esse problema então, seríamos usar a pilha de mínimo.
Como funciona?
A pilha de mínimo usa um valor auxiliar para armazenar o menor elemento até a inserção atual, podemos usar um stack<pair<int,int>> ou duas stack<int>.
O algoritmo então inicia a inserção de N elementos, e para cada inserção de elemento, vamos verificar se o elemento da stack auxiliar é menor ou maior que o da original, e guardaremos o de menor valor na stack auxiliar.
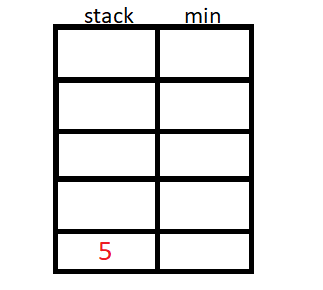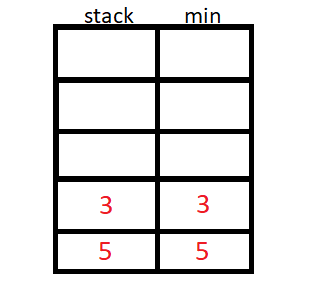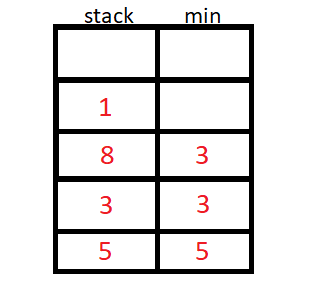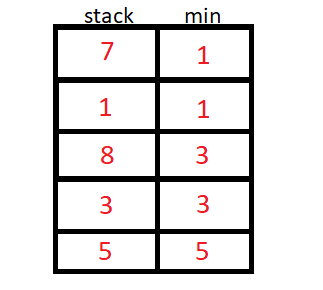
Implementação
#include <bits/stdc++.h>
using namespace std;
int main(){
stack<pair<int,int>> st;
int n; cin>>n;
// recebemos n números
for(int i=0; i<n; i++){
int num;
cin>>num;
if(st.empty()){
// num sera o menor valor da pilha.second
st.push({num,num});
}else{
// armazenamos o menor valor entre
// o que esta na pilha.second e o num atual
int menor = st.top().second;
menor = min(menor, num);
st.push({num, menor});
}
}
// Para Q consultas
int q; cin>>q;
for(int i=0; i<q; i++){
if(!st.empty()){
// pega o menor valor
int val = st.top().second;
st.pop();
cout<<val<<endl;
}
}
return 0;
}
E a complexidade fica somente O(N+Q), pois agora conseguimos responder em O(1) cada query.
Referências:
Fila
A fila segue o padrão de FIFO (first-in first-out), ao contrário da pilha, o primeiro elemento inserido será o primeiro a ser removido. Ela é muito útil para problemas que precisamos manter os elementos na ordem em que lhes foram dados.
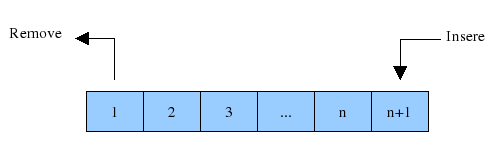
Métodos
push- Adiciona um elemento no fim da fila.front- Retorna o elemento do início da fila.back- Retorna o elemento do final da fila.pop- Remove o elemento do início da fila.empty- Retorna true se estiver vazia, e false caso contrário.size- Retorna quantos elementos tem na fila.
Exemplo
#include <bits/stdc++.h>
using namespace std;
int main(){
queue<int> q;
q.push(9);
q.push(5);
q.push(6);
q.push(1);
q.push(8);
cout<< q.size() <<endl;
while(!q.empty()){
int elemento = q.front();
cout<<elemento<<" ";
q.pop();
}
return 0;
}
Saída
9 5 6 1 8
Fila de Prioridade
Uma fila de prioridade tem como principal característica a ordenação, ela mantém o elemento do topo como sempre sendo o maior (ou o menor) elemento sempre.
Caso esteja fixado para o elemento do topo ser o maior, a fila de prioridade estará em ordem descrescente do topo para baixo. Caso contrário, a ordem será crescente.
Por padrão, ela estará fixado para o elemento do topo ser o maior, logo, estará em ordem decrescente os elementos na fila de prioridade.
As filas de prioridades são muito úteis quando precisamos que nossos elementos sempre estejam ordenados conforme vamos inserindo elementos.
Métodos
push- Adiciona um elemento na fila de prioridade.pop- Remove o elemento do topo da fila de prioridade.top- Retorna o valor do topoempty- Retorna true se a fila estiver vazia, caso contrário, retorna falsesize- Retorna o tamanho da fila de prioridade.
A complexidade de inserção e remoção é O(log(n)), e a de olhar o topo do heap é O(1).
Exemplo
#include <bits/stdc++.h>
using namespace std;
int main(){
priority_queue<int> q;
q.push(9);
q.push(5);
q.push(6);
q.push(1);
q.push(8);
cout<< q.size() <<endl;
while(!q.empty()){
int elemento = q.top();
cout<<elemento<<" ";
q.pop();
}
return 0;
}
Saída
9 8 6 5 1
Ordenação pelo menor valor
Para ordenar pelo menor valor usamos a seguinte sintaxe na declaração:
priority_queue <int, vector<int>, greater<int>> q
Exemplo 2
#include <bits/stdc++.h>
using namespace std;
int main(){
priority_queue <int, vector<int>, greater<int>> q;
q.push(9);
q.push(5);
q.push(6);
q.push(1);
q.push(8);
cout<< q.size() <<endl;
while(!q.empty()){
int elemento = q.top();
cout<<elemento<<" ";
q.pop();
}
return 0;
}
Saída
1 5 6 8 9
ED Não Linear
Subpáginas
Subsecções de ED Não Linear
Map
O map é uma estrutura interessante pois permite “mapear” chaves à valores, e dado uma chave encontrar o seu valor rapidamente (complexidade depende da implementação). Por exemplo, podemos fazer um map com strings de chave e int de valor, sendo possível recuperar o valor inteiro associado a aquela string rapidamente.
Deve-se ter cuidado com o uso de map pois ele é implementado em c++ como um set de pairs, isto é, vai ter complexidade O(log n) para inserir e modificar dados.
Existe também o unordered_map, que é uma estrutura que usa hash. No pior caso é linear, mas em média tem complexidade constante. O seu funcionamento é similar ao do map, com a diferença de que seus elementos não estão ordenados.
Métodos
insert({key, element})- Insere uma chave e um valor no maperase()- Remove uma key ou um iteratorfind(element)- Retorna um iterator da posição do elementcount- Retorna a quantidade de elementos de uma chave específicasize- Retorna o tamanho do mapclear- Limpa todo o conteúdo do Mapbegin- Retorna um iterator para o início do mapend- Retorna um iterator para o final do map
Inicialização
#include <bits/stdc++.h>
using namespace std;
int main(){
// map chave, valor de inteiros
map<int, int> m; // Inicialização de map vazio
map<int, int> m = {{2, 3}, {4, 6}}; // Inicialização de map com valor
m[7] = 3
m[7] ++; // 4
}
Iteração
#include <bits/stdc++.h>
using namespace std;
int main(){
// iterando por métodos iterator
map<int, int> m = {{2, 3}, {4, 6}};
// Printa a chave e o valor em cada linha
for(auto it = m.begin(); it != m.end(); it++){
cout<< it.first <<" "<< it.second<< endl;
}
// tambem pode ser escrito como:
for(auto it: m){
cout<< it.first << " "<< it.second<< endl;
}
}
Saída
2 3
4 6
Apagando elemento
#include <bits/stdc++.h>
using namespace std;
int main(){
// iterando por métodos iterator
map<int, int> m = {{2, 3}, {4, 6}}
m.erase(m.find(2));
m.erase(4);
}
Da primeira maneira, ele apaga em tempo constante, pois está passando um iterator. Da segunda maneira, ele apaga em log(N), pois ele faz uma busca no elemento.
Verificar um elemento
#include <bits/stdc++.h>
using namespace std;
int main(){
// iterando por métodos iterator
map<int, int> m = {{2, 3}, {4, 6}}
if( m.count(2) > 0 ){ // existe uma chave {2}
cout<< "Elemento existe";
}else{
cout<< "Elemento não existe";
}
}
Saída
Elemento existe
Set
A estrutura set é bem parecida com o que conhecemos de conjuntos da matemática; não existem elementos repetidos e a ordem não importa.
A implementação do set, porém, é feita com uma árvore binária de busca, sendo assim permitido inserir, remover e acessar um elemento em O(log n).
A vantagem do set em relação ao vector é que, caso queira inserir um elemento em um vector ordenado e preservar a ordenação, você terá que procurar o lugar que ele deve ser inserido, fazer a inserção e modificar a posição dos elementos à direita dele. Modificar todas as posições à direita tem uma complexidade ruim O(n), então este algoritmo será mais eficiente com o set.
Além da vantagem de eficiência, essas operações com set são feitas com alguns simples métodos!
Métodos
insert(element)- Insere um elemento no Seterase()- Remove uma key ou um iteratorfind(element)- Retorna um iterator da posição do elementcount- Retorna a quantidade de elementos de uma chave específicasize- Retorna o tamanho do setclear- Limpa todo o conteúdo do setbegin- Retorna um iterator para o início do setend- Retorna um iterator para o final do setlower_bound(element)- Retorna um iterator para o primeiro valor >= elementupper_bound(element)- Retorna um iterator para o primeiro valor > element
Exemplo 1
#include <bits/stdc++.h>
using namespace std;
int main() {
set<int> s;
s.insert(3); // insere elemento no set
cout << s.size() << endl; // tamanho do set
// para verificar se um elemento está contido no set ou nao podemos utilizar
// o metodo find; caso nao esteja presente ele retornará o iterator para
// o fim do set
if(s.find(2) == s.end()) {
cout << "O numero 2 nao esta no set" << endl;
}
else {
cout << "O numero 2 esta no set" << endl;
}
if(s.find(3) == s.end()) {
cout << "O numero 3 nao esta no set" << endl;
}
else {
cout << "O numero 3 esta no set" << endl;
}
s.erase(3); // apaga elemento 3 do set
if(s.find(3) == s.end()) {
cout << "O numero 3 nao esta no set" << endl;
}
else {
cout << "O numero 3 esta no set" << endl;
}
return 0;
}
Outro método extremamente útil é o lower_bound (e o upper_bound). O lower_bound recebe um inteiro x como argumento e retorna o menor inteiro maior ou igual a x. Caso não exista, ele retorna um iterator para o fim do set (set.end()).
Exemplo 2
#include <bits/stdc++.h>
using namespace std;
int main() {
set<int> s;
s.insert(3); // insere elemento no set
s.insert(4);
s.insert(5);
s.insert(7);
auto iterator1 = s.lower_bound(6);
// se iterator eh igual a s.end() entao nao existe
if(iterator1 != s.end()) {
int numero = *iterator1;
cout << "menor inteiro maior ou igual a 6 eh " << numero << endl;
}
else {
cout << "nao existe inteiro numero maior ou igual a 6" << endl;
}
auto iterator2 = s.lower_bound(9);
// se iterator eh igual a s.end() entao nao existe
if(iterator2 != s.end()) {
int numero = *iterator2;
cout << "menor inteiro maior ou igual a 9 eh " << numero << endl;
}
else {
cout << "nao existe inteiro numero maior ou igual a 9" << endl;
}
return 0;
}
Na verdade, você pode utilizar o lower_bound para qualquer tipo que implemente a operação “<”, como por exemplo o pair<int, int>.
Estruturas de Dados
Subsecções de Estruturas de Dados
Delta Encoding
Problemas de atualização em intervalos
Suponha que você se depare com um problema do seguinte tipo:
Você recebe um vetor v , inicialmente com todos seus números zerados, e q queries. cada query virá representada por 3 inteiros (l,r,x). Ao receber cada query, a mudança esperada é: “Para cada número no vetor, seja i o seu índice. Se l <= i <= r, v[i] deve ter x adicionado ao seu valor. Ao final do programa, deve-se imprimir o vetor todo com seus valores atualizados.
A primeira solução que já vem a cabeça é a seguinte:
int n,q;
scanf("%d %d",&n,&q);
vi v(n,0);
for (int i = 0; i < q; ++i){
int l,r,x;
scanf("%d %d %d",&l,&r,&x);
for (int j = l; j <= r; ++j){
v[j] += x;
}
}
Nessa solução, para cada uma das q queries, o pior caso seria l = 0 e r = n-1, que faz o laço interno iterar n vezes, o que nos dá uma complexidade O(n*q). Precisamos ser mais rápidos.
Definição
Delta encoding é uma técnica para resolver problemas desse tipo. Precisamos fazer atualizações em intervalos, mas como o vetor só precisa ser visualizado no final, o que fazemos é fazer todas de uma vez só no final. A ideia por trás dessa solução funciona da seguinte forma: Vamos criar um vetor auxiliar delta, que é o vetor que vai acumular as atualizações.
Atualização do intervalo (l,r)
Dessa forma, quando estivermos lendo uma query (l,r,x), faremos o seguinte:
vector<int> delta(n,0);
for(int i = 0; i < q; i++){
int l,r,x;
scanf("%d %d %d",&l,&r,&x);
delta[l] += x;
delta[r+1] -= x;
}
O trecho de código acima é o delta encoding por si só, o nome é esse porque estamos codificando a informação de que precisamos atualizar aquele intervalo. A parte interessante, é que nesse laço, nossa atualização funciona em O(1).
Obtendo os valores após várias atualizações
Tendo as informações organizadas dessa forma, isso nos permite percorrer o vetor delta da esquerda pra direita obtendo os valores finais do vetor, em O(n).
Isso é feito criando uma variável atual, inicializada com 0. Então, enquanto percorremos o vetor, na i-ésima iteração, sempre somamos a essa variável delta[i], após isso, a configuração final de v[i] será o valor de atual.
Então, é por esse motivo que guardamos a informação daquela forma no vetor. Como vamos percorrer da esquerda pra direita, quando fazemos v[l] += x, estamos dizendo, quando você passar no índice l, você deve adicionar mais x a resposta. E quando fazemos v[r+1] -= x, dizemos: quando seu índice for maior que r, pare de considerar x no resultado.
Dessa forma, a versão final:
vector<int> delta(n+5,0);
vector<int> v(n);
for(int i = 0; i < q; i++){
int l,r,x;
scanf("%d %d %d",&l,&r,&x);
delta[l] += x;
delta[r+1] -= x;
}
int atual = 0;
for(int i = 0; i < n; i++){
atual += delta[i];
v[i] = atual;
}
for(int i = 0; i < n; i++){
printf("%d ",v[i]);
}
printf("\n");
Ressalvas
Análogo as somas prefixas, mas de forma inversa, essa ED processa atualizações em intervalo muito rapidamente O(1), porém, quando é necessário saber os valores do vetor, e há atualizações pendentes, é necessário percorrer novamente o vetor todo O(n), então essa ED funciona melhor com muitas atualizações e poucas consultas.
Soma de Prefixos
Problemas de consulta em intervalos
Suponha que você se depare com o seguinte problema:
É dado um vetor V, com n números inteiros, em seguida, um número q de consultas que serão feitas nesse vetor. Cada consulta consiste de um par de inteiros (l,r), representando um intervalo, a resposta para cada consulta é a soma dos inteiros nesse intervalo(inclusivo).
Até agora, em qual complexidade sabemos resolver esse problema?
A solução simples seria:
int n;
int q;
cin >> n;
vector<int> v(n);
// leitura dos elementos
for(int i = 0; i < n; i++){
scanf("%d",v+i);
}
cin >> q;
// respondendo as consultas
for(int i = 0; i < q; i++){
int l, r;
scanf("%d %d",&l,&r);
int soma = 0;
for(int j = l; j <= r; j++){
soma += v[j];
}
cout << soma << endl;
}
Essa solução teria complexidade O(q*n) aonde q é o número de consultas, e n o tamanho do vetor.
Definição
O vetor de somas prefixas é uma ED que podemos usar para resolver esse tipo de problema de forma mais eficiente. A ideia é construir um vetor P tal que P[i] representa a soma do índice 0 até o índice i.
Tendo essas informações, para responder uma consulta (l,r) podemos usar a seguinte ideia: sabe-se que em P[r] temos a resposta para a consulta (0,r), com isso, podemos agora subtrair a parte que não nos interessa, (0,l-1) ou P[l-1].
Construção
A construção do vetor de somas prefixas em v tem complexidade O(n).
vector<int> psum(v.size(), v[0]);
for(int i = 1; i < v.size(); i++) {
psum[i] = v[i] + psum[i-1];
}
Resposta de consulta (l,r)
A resposta às consultas tem complexidade constante, já que são só acessos ao vetor. Apenas tem-se que tomar cuidado quando l = 0.
int sum(int l, int r){
if(l == 0)
return psum[r];
else
return psum[r] - psum[l-1];
}
Ressalvas
Vale lembrar que essa ED é mais interessante de ser usada quando não há (ou há poucas) atualizações nos valores do vetor, caso haja, é necessário recomputar as somas prefixas do vetor todo em O(n), o que não é uma complexidade atrativa.
Além disso, esse raciocínio não precisa se extender apenas a somas, funciona para operações como xor, por exemplo.
Segment Trees
Segment tree (Segtree) é outra estrutura de dados para lidar com problemas de consulta em intervalos. O que tornas as segtrees poderosas é sua capacidade de fazer atualização e consulta em intervalos em complexidade O(log n), além do tipo da consulta ser bem abrangente.
A ideia é a seguinte: Criamos uma árvore, de forma que cada nodo representa a informação que desejamos saber a respeito de um segmento do vetor, e tem dois filhos, um filho representa a metade esquerda desse intervalo, e o outro, a metade direita. Esse processo recursa até que os intervalos atinjam tamanho 1.
Aqui há uma demonstação visual de como funciona: https://visualgo.net/en/segmenttree
É interessante entender o funcionamento da segtree pois, por mais que tenhamos o código pronto, quando mudamos de operação ou precisamos inserir long longs, será necessário mexer na sua estrutura interna.
Representação
Nossa segtree será representada como um vetor. Cada nodo terá um id nesse vetor, e o conteúdo dessa posição representa a informação que aquele nodo guarda. A raiz da segtree será o nodo 0, que guarda a informação sobre o vetor todo. A partir do índice id de um nodo, podemos obter os filhos sem colisões da seguinte forma: índice dos filhos esquerdo e direito são (id*2 + 1,id*2 +2), respectivamente.
vector<int> st;
int size;
Operação
Essa função define que informação queremos saber a respeito dos elementos do vetor. Nese caso é uma segtree que computa o máximo de intervalos, mas poderia ser soma, mínimo, produto, xor, gcd, mmc(lcm), or e and lógicos etc.
int f(int a, int b){
return max(a,b);
}
Elemento neutro
O elemento neutro depende da operação. Como queremos saber os máximos, o elemento neutro dessa operação seria um número muito baixo, que nunca será o máximo.
Caso não saiba a definição de elemento neutro, a definição é a seguinte: e é um elemento neutro da operação f se f(e,x) = x para todo x.
Caso fosse uma soma, nosso elemento neutro seria 0, caso fosse um produto, seria 1, etc..
int el_neutro = -(1e9 + 7);
Consulta
A função recursiva abaixo responde às consultas na segtree. Cada parâmetro tem o seguinte significado:
sti: id do nodo que estamos na segment treestl: limite inferior do intervalo que aquele nodo representa(inclusivo)str: limite superior do intervalo que aquele nodo representa(inclusivo)l: limite inferior do intervalo que queremos fazer a consultar: limite superior do intervalo que queremos fazer a consulta
int query(int sti, int stl, int str, int l, int r){
//O nodo está fora do intervalo que estamos interessados, retorne o elemento neutro que não afeta a consulta
if(str < l || r < stl)
return el_neutro;
// O nodo está completamente incluído no intervalos que estamos interessados, retorne a informação contida naquele nodo.
if(stl >= l and str <= r)
return st[sti];
// Se chegarmos aqui, é porque esse Nodo está parcialmente contido no intervalo que estamos interessados. Então, continuamos procurando nos filhos.
int mid = (str+stl)/2;
return f(query(sti*2+1,stl,mid,l,r),query(sti*2+2,mid+1,str,l,r));
}
Atualização
Essa função atualiza um elemento da segtree. Cada parâmetro tem o seguinte significado:
sti: id do nodo que estamos na segment treestl: limite inferior do intervalo que aquele nodo representa(inclusivo)str: limite superior do intervalo que aquele nodo representa(inclusivo)i: índice do vetor que queremos atualizaramm: novo valor daquele índice no vetor
void update(int sti, int stl, int str, int i, int amm){
// Chegamos no índice que queremos, vamos atualizar o valor
if(stl == i and str == i){
st[sti] = amm;
return;
}
// O intervalo que estamos não contem o índice que queremos atualizar, retorne
if(stl > i or str < i)
return;
// O intervalo contém o índice, mas temos que chegar no nodo específico, recurse para os filhos.
int mid = (stl + str)/2;
update(sti*2+1,stl,mid,i,amm);
update(sti*2+2,mid+1,str,i,amm);
// Após os filhos mais em baixo, precisamos atualizar o valor desse nodo
st[sti] = f(st[sti*2+1],st[sti*2+2]);
}
Declaração
Essa é a classe com as funcionalidades implementadas.
class SegTree{
vector<int> st;
int size;
int el_neutro = -(1e9 + 7);
int f(int a, int b){
return max(a,b);
}
int query(int sti, int stl, int str, int l, int r){
if(str < l || r < stl)
return el_neutro;
if(stl >= l and str <= r)
return st[sti];
int mid = (str+stl)/2;
return f(query(sti*2+1,stl,mid,l,r),query(sti*2+2,mid+1,str,l,r));
}
void update(int sti, int stl, int str, int i, int amm){
if(stl == i and str == i){
st[sti] += amm;
return;
}
if(stl > i or str < i)
return;
int mid = (stl + str)/2;
update(sti*2+1,stl,mid,i,amm);
update(sti*2+2,mid+1,str,i,amm);
st[sti] = f(st[sti*2+1],st[sti*2+2]);
}
public:
SegTree(int n): st(4*n,0){size = n;}
int query(int l, int r){return query(0,0,size-1,l,r);}
void update(int i, int amm){update(0,0,size-1,i,amm);}
};
Interface
Os métodos que mostramos são todos internos da segtree, na hora de chama-los, não precisamos passar tantos parâmetros assim.
public:
SegTree(int n): st(4*n,0){size = n;}
int query(int l, int r){return query(0,0,size-1,l,r);}
void update(int i, int amm){update(0,0,size-1,i,amm);}
SegTree
Construtor, recebe o tamanho do vetor.
query
Executa uma consulta, recebe o intervalo(l,r) da consulta, retorna o resultado.
update
Atualiza um índice no vetor recebe o índice e o novo valor.
Construção
vector<int> v;
SegTree st(v.size());
for(int i = 0; i< v.size();i++){
st.update(i,v[i]);
}
Atualizações em intervalos
A segtree que temos até agora faz atualização de uma posição no vetor e consulta de qualquer em intervalo, em O(log n). Mas e se precisarmos atualizar um intervalo, por exemplo: “Todos os elementos da posição 1 até 10 recebem 2”. Assim, a melhor forma que teríamos de fazer isso seria
SegTree st(n);
// preenche segtree
for(int i = 1 ; i <= 10; i++){
st.update(i,2);
}
O que tem complexidade O(n * log n). Precisamos fazer isso mais rápido.
Lazy progapation
Lazy propagation é uma alteração na segtree que nos permite fazer atualizações em intervalos em O(log n).
A ideia
Em nossa abordagem anterior, o que tornava a execução lenta é que procurávamos o nodo responsável por cada elemento que precisava ser atualizado.
Para acelerar esse processo, podemos usar uma ideia parecida com a da consulta, em vez de atualizar individualmente os elementos, podemos atualizar a resposta nos intervalos que os contém, e postergar a atualização nos filhos.
Para implementar lazy propagation, cada configuração de segtree vai requerer uma implementação um pouco diferente, por isso, será necessário entender o que cada parte do código está fazendo.
O exemplo a seguir será de uma segtree de soma, aonde a atualização de intervalo vai setar todos os elementos para um qualquer.
vetor de lazy
A ideia é introduzir um vetor extra com o seguinte significado: Quando eu passar no nodo identificado por id, em uma consulta, ou outra atualização, preciso atualizar seu valor para lazy[id]. O vetor has indica se há uma atualização para ser feita naquele nodo.
vector<int> st;
vector<int> lazy;
vector<bool> has;
int size;
A propagação
A função de propagação é a função que atualiza o valor de um nodo, e posterga a atualização para os filhos. Precisamos chamar essa função toda vez que passamos por algum nodo.
void propagate(int sti, int stl, int str){
// Se há algo para atualizar, atualize()
if(has[sti])
//O valor desse nodo da segtree será (número de elementos que esse intervalo representa vezes novo valor de cada elemento do intervalo)
st[sti] = lazy[sti] * (str - stl + 1);
// Se o nó representa um segmento de tamanho maior que 1, isto é, não é terminal, propague a atualização para os filhos.
if(stl != str){
lazy[sti*2 + 1] = lazy[sti];
lazy[sti*2 + 2] = lazy[sti];
has[sti*2 + 1] = true;
has[sti*2 + 2] = true;
}
// agora não é mais necessário atualizar esse nodo
has[sti] = false;
}
}
A função de atualização em intervalo
Essa é a função que realiza a atualização de intervalos. O significado dos argumentos é:
sti: id do nodo que estamos na segment treestl: limite inferior do intervalo que aquele nodo representa(inclusivo)str: limite superior do intervalo que aquele nodo representa(inclusivo)l: limite inferior do intervalo que queremos atualizar no vetorr: limite superior do intervalo que queremos atualizar no vetoramm: novo valor dos elementos nesse intervalo
void update_range(int sti, int stl, int str, int l,int r, int amm){
if(stl >= l and str <= r){
// O valor que será atribuido a todo elemento no intervalo
lazy[sti] = amm;
has[sti] = true;
propagate(sti, stl, str);
return;
}
if(stl > r or str < l)
return;
int mid = (stl + str)/2;
update_range(sti*2+1,stl,mid,l,r,amm);
update_range(sti*2+2,mid+1,str,l,r,amm);
st[sti] = f(st[sti*2+1],st[sti*2+2]);
}
Versão final
Essa é a versão final da nossa ED.
class SegTree{
vector<int> st;
vector<int> lazy;
vector<bool> has;
int size;
int el_neutro = 0;
int f(int a, int b){
return a + b;
}
void propagate(int sti, int stl, int str){
if(has[sti]){
st[sti] = lazy[sti] * (str - stl + 1);
if(stl != str){
lazy[sti*2 + 1] = lazy[sti];
lazy[sti*2 + 2] = lazy[sti];
has[sti*2 + 1] = true;
has[sti*2 + 2] = true;
}
has[sti] = false;
}
}
int query(int sti, int stl, int str, int l, int r){
propagate(sti, stl, str);
if(str < l || r < stl)
return el_neutro;
if(stl >= l and str <= r)
return st[sti];
int mid = (str+stl)/2;
return f(query(sti*2+1,stl,mid,l,r),query(sti*2+2,mid+1,str,l,r));
}
void update_range(int sti, int stl, int str, int l,int r, int amm){
if(stl >= l and str <= r){
lazy[sti] = amm;
has[sti] = true;
propagate(sti, stl, str);
return;
}
if(stl > r or str < l)
return;
int mid = (stl + str)/2;
update_range(sti*2+1,stl,mid,l,r,amm);
update_range(sti*2+2,mid+1,str,l,r,amm);
st[sti] = f(st[sti*2+1],st[sti*2+2]);
}
public:
SegTree(int n): st(4*n,0), lazy(4*n,0),has(4*n,false){size = n;}
int query(int l, int r){return query(0,0,size-1,l,r);}
void update_range(int l, int r, int amm){update_range(0,0,size-1,l,r,amm);}
};
Problemas recomendados
Sparse Table
Nesse tutorial vamos falar sobre uma estrutura de dados chamada Sparse Table, que é uma estrutura de dados poderosa para resolvermos range queries de algumas operações específicas em complexidades superiores as de uma Segment Tree por exemplo.
Por exemplo, uma Sparse Table conseque resolver range minimum(ou maximum) query em O(1), enquanto numa segment tree precisaríamos de O(log n). Outro exemplo poderia ser range query de gcd, numa Segment Tree podemos resolver range queries de GCD em O(log^2 n), já na sparse table conseguimos isso em O(log n). No geral, quando a operação da range query tem uma propriedade chamada idempotência, podemos tirar um log da complexidade usando a Sparse Table.
Idempotência
A propriedade que uma operação precisa ter para que possamos ganhar tempo de execução usando a Sparse Table é a idempotência. Na definição que estamos levando em consideração, uma operação op (binária) é idempotente quando para todo x e todo y, op(x,y) = op(x,op(x,y)). Poderíamos dar uma definição mais precisa porém o que precisamos saber é que numa operação idempotente, aplicar a operação uma vez é o mesmo que aplicar 2,3,4,… qualquer número de vezes maior que 0.
A operação min possui essa propriedade, para qualquer x,y, min(x,y) = min(x,min(x,y)). Outro exemplo é o próprio gcd como mencionado acima. para qualquer x,y, gcd(x,y) = gcd(x,gcd(x,y)).
Mas essa propriedade não é verdade para a operação de soma, por exemplo, seja sum(x,y) = x + y, sum(3,4) != sum(3,sum(3,4)), aplicar a operação mais de uma vez com os mesmos argumentos a direita(ou a esquerda) resulta num resultado diferente, então soma não é idempotente. Na verdade as operações mais comuns vão ser GCD e min/max, mas é importante saber a propriedade para entender porque a ideia que vamos usar funciona e também caso haja uma operação meio maluca que seja idempotente saber se consegue montar a Sparse table sobre ela.
O pulo do gato
Imagine que tenhamos uma função mágica, chamada dp(n,k), que retorna a operação aplicada no intervalo [n, n + (2^k) - 1].
k = 0, [n, n]
k = 1, [n, n + 1]
k = 2, [n, n + 3]
k = 3, [n, n + 7]
.
.
Então se a operação for min, vai ser o mínimo dos elementos nesse intervalo, se for gcd vai ser o gcd entre todos os número desse intervalo etc. Certo então com essa função, vamos fingir que recebemos uma min query para o intervalo [4, 17] em um vetor.
Como a operação é idempotente, podemos fazer o seguinte. A resposta vai ser min(dp(4,3), dp(10,3)),
[0, 1, 2, 3, (4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17)]
[1, 3, 2, 5, (9, 6, 8, 0, 1, 2, 40, 51, 2, 4, 63, 20, 2, 4)]
O intervalo que estamos interessados está demarcado com um parêntese. Bem, dp(4, 3) = 0, e dp(10,3) = 2, e min(0,2) = 0, que realmente é o mínimo do intervalo. Se a query fosse no intervalo [4,10] poderíamos fazer min(dp(4,2), dp(7,2)), e assim por diante.
Então o que nós estamos fazendo aqui é selecionando uma potencia de dois e duas posições aonde duas chamadas a essa função mágica vão ser suficientes para cobrir exatamente o intervalo que estamos interessados. E a operação precisa ser idempotente porque como estamos selecionando apenas intervalos que tem tamanhos de potências de dois, no caso geral não conseguimos selecionar dois intervalos que não tenham interseção, e caso a operação não seja idempotente, isso fará com que a interseção seja contada duas vezes, fazendo então com que essa ideia não funcione. Voltaremos mais tarde na implementação de como selecionar essas potências.
Então a complexidade que temos até então para resolver consultas é a seguinte: O(k + 2*q) aonde k é o custo da operação, e q é o custo da nossa função mágica. Veremos que conseguimos com programação dinâmica precomputar os valores pra essa função fazendo com que as chamadas a ela tenham tempo constante. Como min() tem tempo constante de gcd() tempo log, é assim que resultamos nas complexidades mencionadas no começo do texto.
Recorrência
Esta é a recorrência da programação dinâmica, nessa recorrência, estamos apenas dizendo o seguinte: O resultado da operação em um intervalo é o resultado da primeira metade combinado com o resultado da segunda metade.
int dp(int i, int k) {
if(k == 0) {
return v[i];
}
return op(dp(i,k-1),dp(i + (1 << (k-1)). k-1));
}
Versão recursiva
int memo[SIZE][log2(SIZE)+1];
vector<int> v(SIZE);
int dp(int i, int k) {
if(i >= SIZE) return 0;
if(k == 0) {
return v[i];
}
if(memo[i][k] != -1) return memo[i][k];
return memo[i][k] = min(dp(i,k-1),dp(i + (1 << (k-1)), k-1));
}
Versão iterativa
int memo[SIZE][log2(SIZE)+1];
vector<int> v(SIZE);
for(int i = 0; i < SIZE; i++) {
memo[i][0] = v[i];
}
for(int k = 1; k <= log2(SIZE); k++) {
for(int i = 0; i < SIZE; i++) {
if(i + (1 << k -1) >= SIZE) {
memo[i][k] = memo[i][k-1];
} else {
memo[i][k] = op(memo[i][k-1], memo[i + (1 << (k-1))][k-1]);
}
}
}
Precisamos apenas computar para potências até log2(SIZE) + 1 porque potências maiores que essa com certeza já são maiores que o vetor.
Outro detalhe de implementação é que temos que tomar cuidado para não acessar fora do vetor, algumas alternativas que temos podem ser por exemplo adicionar um if(i >= SIZE) return 0; na versão recusiva. Na versão iterativa fazemos de maneira análoga.
Estamos preenchendo uma tabela de tamanho O(n log n) aonde n é o tamanho da árvore, para preencher cada célula dessa tabela fazemos operações constantes e uma chamada a op, então a complexidade de montarmos essa tabela para responder as queries é O(n log n * K), aonde K é a complexidade de op.
Ajustando a consulta
Acima demos alguns exemplos de como podemos usar a recorrência que definimos para computar intervalos específicos, por exemplo para [4,17], escolhemos (4,3) e (10,7). O intervalo em questão tem tamanho 14, então a menor potência de 2 que podemos usar para cobri-lo é 8(2^3). Em geral essa menor potência pode ser calculada pela expressão log2(b-a), aonde log2(x) é o chão do logaritmo de x na base 2 e assumimos que b > a.
log2(13) = 3
log2(14) = 3
log2(15) = 3
log2(16) = 4
.
.
.
E sobre as posições da query, a primeira sempre será no começo do intervalo, e a segunda temos que ajustar de forma que o último elemento levado em consideração seja o último.
int query(int a, int b) {
int lg = log2(b-a);
return F(tb[a][lg],tb[1 + b-(1 << lg)][lg])
}
Conteúdo complementar
https://www.youtube.com/watch?v=EKcQt-74bNw
Exercícios recomendados
Algoritmos
Subpáginas
Subsecções de Algoritmos
Busca Binária
Busca binária é um algoritmo de divisão e conquista usado em sua maior parte para minimizar o tempo de uma busca linear. Na busca binária sempre estamos procurando o “o maior x valor que satisfaz uma condição c(x)” ou “o menor x valor que satisfaz uma condição c(x)”, retornaremos nesse ponto depois no texto.
Imagine você com um livro de 1000 páginas em mãos no momento em que o professor pede para que o abra no começo do capitulo 6 seção 4. Existem várias maneiras de se alcançar a página certa. Uma delas é ir de uma em uma até que se alcance a página desejada. Outra maneira é ir pulando alguns blocos de páginas, se você está numa página depois do começo do capitulo 6 seção 4 pula algumas páginas para tras, se você está numa página antes, pula algumas páginas para frente.
Perceba que no exemplo acima uma busca linear (passar de página em página) demoraria muito mais do que ir pulando algumas partes do livro. E fazendo da segunda maneira involuntariamente você acaba aplicando uma versão primitiva do que chamamos de busca binária.
O algortimo
Usando a mesma ideia do livro porém agora em uma linguagem mais computacional. No lugar de 1000 páginas podemos ter um vetor de 1000 posições onde a i-ésima tem um pair <capitulo, seção> da pagina i, por exemplo, se a página 125 faz parte do capítulo 4 seção 2 então v[125] = make_pair(4, 2);. E digamos que o capítulo 6 seção 4 está na página 375(que não sabemos no começo da busca).
Primeiro podemos, por exemplo, para a página 400. A partir do pair daquela posição aprendemos que o que procuramos está antes de 400, então agora não precisamos procurar a resposta no intervalo [1, 1000] e sim no intervalo [1, 399]. Podemos fazer um segundo chute na posicao 300, por exemplo pois podemos chutar em qualquer posição do intervalo, e depois de olhar v[300] aprendemos que a resposta está no intervalo [301, 399]. Podemos então chutar na página 375 e encontrar que esta é a resposta que procuramos.
O único problema do que foi descrito acima é determinar como chutar o elemento dentro do intervalo já que os chutes foram meio aleatórios. O primeiro chute foi no elemento 400 num intervalo [1, 1000], depois de olhar o elemento poderíamos passar a ter que olhar o intervalo [1, 399](se o que procuramos está antes) ou [401, 1000](se o que procuramos está depois), tivemos sorte e caimos no primeiro caso mas no pior caso poderíamos cair no intervalo maior. O jeito de garantirmos de no pior caso sempre irmos para um intervalo de menor tamanho possivel é chutar de uma forma a dividir o intervalo em 2 intervalos de tamanhos (aproximadamente) iguais. Podemos fazer isso só chutando na metade do intervalo, assim é melhor fazer o primeiro chuta na posição 500 e nao 400.
Condições para aplicar busca binária
Nem sempre é possível aplicar busca binária para encontrar uma resposta: um exemplo seria um livro cujos capitulos e seçoes nao estão em ordem crescente. Nessa situação, não poderiamos mais ter certeza que um capitulo ou seção maior estaria a direita.
Como mencionamos acima, na busca binária estamos procurando o maior ou menor valor que satisfaz uma propriedade. Então por exemplo, no exemplo acima, estamos buscando pelo menor índice(página) do vetor(livro) que satisfaz a condição “estar num (capítulo, seção) maior ou igual a (6,4)”, porque a primeira página que satisfazer essa propriedade será o início do capítulo 6 seção 4. Considere agora o outro exemplo de aplicarmos busca binaria no vetor para descobrir se um elemento x esta lá ou não. Uma maneira de fazer isso seria procurar pelo menor elemento y que seja maior ou igual x, se y for igual a x, então x está no vetor, caso contrário x não está no vetor.
Dizemos que é possível aplicar busca binária em um problema quando a checagem se um valor satisfaz as condições apresenta monotonicidade. Formalmente, monotonicidade pode ser definida da seguinte forma. Seja check(x) uma função que verifica uma propriedade de x Se para todo x, check(x) = true implica check(x+1) = true, ou para todo x, check(x) = false implica check(x+1) = false, então a função check é monótona.
Então, se x = 11 e o vetor v = [1,2,3,5, 8, 11, 12, 14, 16] observe o que acontece com o comportamento de uma função check que checa se um elemento é maior ou igual a x.
bool check(int val) {
return val >= x;
}
[1,2,3,5,8,11,12,14,16]
[0,0,0,0,0,1,1,1,1,1]
Então se colocarmos graficamente os resultados de uma função check monotona, veremos exatamente isso, ou um monte de valores 0s e a partir de certo ponto todos são 1s, ou o contrário, um monte de 1s e a partir de certo ponto todos são 0s. No exemplo a cima é a primeira possibilidade.
Então a função check para essa situação é monótona, e isso é relevante porque se um valor do vetor satisfizer a condição, todos os valores a direita também vão satisfazê-la, e de forma análoga, todos os valores a esquerda de um índice que não satisfaz a condição, também não vão satisfazer, e é isso que nos permite aplicar busca binária. E a função check só se torna monótona nesse exemplo quando o vetor está ordenado, por isso busca binária só é feita em vetores ordenados : ).
Então o que faremos é chutar intervalo aonde a resposta com certeza estará no começo, fazemos então várias interações checando no meio, e dependendo da resposta, descartamos os elementos a direita ou a esquerda, mas sempre dividimos o tamanho do intervalo por 2, até que o intervalo tenha tamanho 1.
Complexidade
Tudo muito massa, mas falta a complexidade! Depois de saber isso podemos começar a aplicar esse algoritmo nos problemas por ae :)
por enquanto nosso algoritmo de maneira abstrata é o seguinte
while(tamanho do intervalo que a resposta pode estar != 1) {
chuta no meio e descarta a metade da direita ou da esquerda(dependendo do resultado), dividindo o intervalo por 2;
}
Suponha um vetor ordenado de tamanho N onde vamos aplicar o algoritmo de busca binária e o valor procurado não está presente no vetor (pior caso). Na nossa primeira iteração iremos dividir o vetor em 2 partes ou seja teremos N/2 elementos restantes, na segunda iteração iremos dividir do que restou e teremos (N/2)/2 ou seja N/4, seguindo essa lógica na K-ésima iteração vamos dividir o tamanho do vetor K vezes por 2, ou seja, N/(2^K) e como estamos calculando complexidade temos que pensar no pior caso, quando chegarmos no ponto onde teremos um espaço de apenas 1 elemento(e verificamos que o elemento não está no vetor). O que estamos buscando para saber a complexidade é K (quantidade de passos) para o pior caso então temos que N/(2^K) = 1 daí temos que N = 2^K e tirando o log2 dos dois lados temos que K = log2(N). Então no pior caso nosso algortimo demora O(log2(N)) passos, N sendo o tamanho do intervalo inicial. Se a função de checagem tiver uma complexidade O(f(x)), então teremos complexidade no total O(log2(N) * f(x))*.
Código base para busca binária
Há várias maneiras de se implementar busca binária, vamos apresentar várias delas. Vamos usar sempre a função check em separado, os jeitos de implementar diferente são apenas do corpo da busca binária.
bool check(int val){
// nessa função checamos se uma resposta satisfaz as condições para ser uma resposta válida, e retornamos um booleano dependendo disso.
}
Tipo 1
Valor mínimo (Menor valor que torna check verdadeiro)
int l = a;// sei que a resposta não é menos que a
int r = b;// sei que a resposta não é mais que b (as vezes esse chute tem que ser bom, para evitar overflow)
while(r > l+1){// repita enquanto o intervalo tiver tamanho > 2
int mid = (l + r)/2;
if(check(mid)){ // mid é válido
r = mid; // como queremos minimizar a resposta, e mid é uma resposta válida
//descartamos tudo a direita de mid (mas não mid)
}
else{
l = mid+1; // Se mid não é válido, descartamos ele e tudo abaixo.
}
}
// Ao final desse laço, a resposta pode estar em l ou r.
// Queremos minimizar a resposta, então se l for válido,
// ficaremos com l, e caso contrário, com r
int ans = r;
if(check(l)){
ans = l;
}
Valor máximo (Maior valor que torna check verdadeiro)
int l = a;
int r = b;
while(r > l+1){
int mid = (l + r)/2;
if(check(mid)){// mid é válido
l = mid; // como queremos maximizar a resposta, e mid é uma resposta válida
//descartamos tudo a esquerda de mid (mas não mid)
}
else{
r = mid-1; // Se mid não é válido, descartamos ele e tudo acima.
}
}
int ans = r;
if(check(l)){
ans = l;
}
Tipo2
Valor mínimo
int l = a;
int r = b;
while (l < r) {
int mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid + 1;
}
// a resposta fica em l
Valor máximo
É fácil alterar o código de valor mínimo para encontrar o valor máximo:
Imagine que uma função de check dê o resultado [1,1,1,0,0]. Veja que encontrar o último 1
nesse array é equivalente a encontrar o primeiro 0 e subtrair 1 da posição! Assim, podemos aplicar
a busca binária de valor mínimo no valor contrário do checker (!check(mid)) e subtrair 1 da resposta ao final.
int l = a;
int r = b;
while (l < r) {
int mid = (l + r) / 2;
if (!check(mid)) r = mid; // check vira !check
else l = mid + 1;
}
// a resposta fica em l-1
Detalhe: como usamos l-1 no final, a busca não inclui b, ou seja, buscamos no intervalo [a, b).
Exemplos de aplicação
Implementação de lower_bound
Consideremos o problema de achar o indice do primeiro elemento maior ou igual um x num vetor v de tamanho n.
int v[MAXN], n; // vetor global para facilitar o código
// funcao que retorna se id é uma resposta válida pro nosso problema
bool check(int id, int x){
return v[id] >= x;
}
// retorna o indice do primeiro elemento >= x, considerando que o vetor v está ordenado
// se todos os elementos sao menores que x, retorna -1
int lower_bound(int x){
int L, R, ans;
L = 0; // começo do intervalo que consideraremos
R = n-1; // fim do intervalo que consideraremos
ans = n; // começamos a resposta com um valor fora do vetor, inválido para marcar se conseguimos achar alguma resposta ou nao
while(L <= R){ // enquanto tiver algum número no intervalo
int mid = (L+R)/2;
if(check(mid, x)){ // se esse mid é uma resposta apropriada
ans = mid; // achamos uma nova resposta para o problema
R = mid-1; // se mid é uma resposta temos que tentar procurar uma resposta menor(nesse problema em especifico)
}
else{ // se mid nao é uma resposta pro nosso problema
L = mid+1; // precisamos procurar em indices maiores(neste problema)
}
}
if(ans == n) return -1; // se ans ainda é n depois da busca binária, então nunca achamos resposta
return ans;
}
Perceba que se quisermos achar o indice do último elemento maior ou igual um x num vetor v de tamanho n.
long long
int v[MAXN], n; // vetor global para facilitar o código
// funcao que retorna se id é uma resposta válida pro nosso problema
bool check(int id, int x){
return v[id] >= x;
}
// retorna o indice do primeiro elemento >= x, considerando que o vetor v está ordenado
// se todos os elementos sao menores que x, retorna -1
int lower_bound(int x){
int L, R, ans;
L = 0; // começo do intervalo que consideraremos
R = n-1; // fim do intervalo que consideraremos
ans = n; // começamos a resposta com um valor fora do vetor, inválido para marcar se conseguimos achar alguma resposta ou nao
while(L <= R){ // enquanto tiver algum número no intervalo
int mid = (L+R)/2;
if(check(mid, x)){ // se esse mid é uma resposta apropriada
ans = mid; // achamos uma nova resposta para o problema
L = mid+1; // se mid é uma resposta temos que tentar procurar uma resposta maior(nesse problema em especifico)
}
else{ // se mid nao é uma resposta pro nosso problema
R = mid-1; // precisamos procurar em indices menores(neste problema)
}
}
if(ans == n) return -1; // se ans ainda é n depois da busca binária, então nunca achamos resposta
return ans;
}
Em ambos os exemplos a complexidade de checar se mid é uma resposta válida para o problema é O(1). Portanto a complexidade total é O(lg n).
Muitas pessoas ja viram o exemplo de realizar busca binária em vetores, mas quando se fala em busca binária na resposta, ficam confusas. Na verdade, busca binária em vetores é busca binária na resposta, mas a resposta é um índice.
Material complementar
Exercícios recomendados
Estes exercícios não estão necessariamente em ordem de dificuldade.
- https://codeforces.com/contest/1234/problem/A - Não é necessário busca binária mas é um exercício legal para aprender
- https://codeforces.com/problemset/problem/817/C - Bem interessante, (se x é um numero realmente grande entao x+1 é realmente grande)
- https://codeforces.com/problemset/problem/760/B - Se frodo não consegue ter x de altura então consegue ter x+1 de altura. Cuidado com overflows!
- https://codeforces.com/gym/102346/problem/M - (Tente minimizar o quanto cada competidor come já que a resposta é em função do competidor que mais come)
Grafos
Subpáginas
Subsecções de Grafos
Representação de Grafos
Um dos assuntos mais frequentes são problemas relacionados a grafos, ou que podem ser representados como grafos, apesar de não ser óbvio à primeira vista.
Conceitos
Há diversos tipos e atributos de um grafo:
O que é um grafo?
Um grafo é definido simplesmente por um conjunto de vértices, e outro conjunto de arestas. Essas arestas ligam dois vértices, e podem ter pesos atrelados à elas.
Grafo simples
Grafo simples é um grafo que não cujas arestas não tem peso, não possui loops, e nem arestas múltiplas. Loops são arestas do tipo (u,u), ou seja, que saem do vértice u, e vão para o vértice u. Um grafo com arestas múltiplas é um grafo que tem duas aresta iguais.
Grafos direcionados
Existem grafos direcionados e não direcionados. No caso dos direcionados, significa que cada aresta tem uma direção, ou seja, se é possível chegar de a em b, não significa que é possível chegar de b em a.
Ciclos
A definição de ciclo é um pouco diferente dependendo se o grafo é direcionado ou não.
Caso o grafo não seja direcionado, e hajam dois caminhos diferentes de um vértice a para um vértice b, então há um ciclo.
Caso contrário, ou seja, caso o grafo seja direcionado, para que haja um ciclo é necessário que exista um vértice a tal que seja possível voltar a a partindo dele mesmo.
Conexo
Um grafo conexo é um grafo tal que para dois vértices quaisquer u e w, sempre existe um caminho de u para w.
Componentes conexas
Um grafo que não é conexo pode ter várias componentes conexas (grafos conexos tem somente uma componente). Essencialmente, uma componente conexa é um pedaço conexo do grafo. Esse conceito é usado no caso de grafos não-direcionados.
Componentes fortemente conexas
Já nos casos do grafos direcionados, o termo usado é esse, também chamados por SCCs(Strongly Connectec Components). A definição mais ‘formal’ é a seguinte: dentro de uma componente conexa de um grafo direcionado, para todo vértice a e b, deve ser possível de chegar de b partindo de a e em a partindo de b.
Basicamente o que a definição acima está dizendo é: uma componente fortemente conexa é um ciclo, mas é importante lembrar que se dois ciclos se juntam, formam um ciclo maior, logo, uma componente maior.
Árvore
Uma árvore é um tipo de grafo. Para ser uma árvore, o grafo precisa ser conexo, não ter ciclos e ter n-1 arestas, aonde n é o número de vértices.
DAG
DAG é uma sigla para Directed Acyclic Graph, ou seja, um grafo acíclico e direcionado. É um termo bastante usado.
Grafos bipartidos
Um grafo bipartido é um grafo tal que é possível dividir seus vértices em dois grupos, de forma que só hajam arestas ligando vértices do primeiro ao segundo grupo.
Representação de um grafo
Mas como representar um grafo em código?
Na verdade é bem mais simples do que parece. Para cada vértice, temos que manter apenas uma lista das arestas que saem daquele vértice.
Nessa representação, a i-ésima posição no vector de fora vector<int>, esse vector representam as arestas que saem daquele vértice. Então, cada vértice tem um número associado a ele.
Exemplo

vector<int> graph[7];
graph[4].push_back(6);
graph[6].push_back(4);
graph[4].push_back(5);
graph[5].push_back(4);
graph[4].push_back(3);
graph[3].push_back(4);
graph[2].push_back(3);
graph[3].push_back(2);
graph[2].push_back(5);
graph[5].push_back(2);
graph[4].push_back(6);
graph[6].push_back(4);
graph[2].push_back(1);
graph[1].push_back(2);
// lembrando que no caso de grafos não direcionados, quando adicionamos (a,b) precisamos sempre adicionar (b,a) junto.
Representação da grafos implícitos
Considere o seguinte problema para guiar a explicação: http://codeforces.com/problemset/problem/520/B
A principio, nao parece exatamente muito fácil relacionar esse problema com grafos. Onde estão os vértices e as arestas? Na verdade nesse problema há o que chamamos de grafo implícito.
Podemos considerar os vértices como o número mostrado pelo display, e as arestas como os vértices que consigo alcançar apertando os botões, a partir do vértice que estou. Mas nós não vamos criar uma estrutura de lista de adjacências em memória igual ao caso anterior, não precisamos. A única coisa que precisamos é saber quais vértices podemos atingir a partir de um vértice x, então quando formos percorrer esse grafo implícito, como todos os vértices seguem essa regra, não precisamos criar as arestas propriamente ditas. Apenas sabemos que é possível atingir os vértices x-1 e 2x.
O mesmo ocorre pra representação de jogos de turno, por exemplo jogo da velha ou damas. Podemos considerar uma configuração do tabuleiro como um vértice, e as arestas ligando para todas as configurações possíveis de atingir segundo as regras de jogada.
VideoAulas complementares
https://www.youtube.com/watch?v=zaBhtODEL0w
Exercícios recomendados
- https://www.urionlinejudge.com.br/judge/pt/problems/view/1910 - Caminho mínimo em grafo implícito sem pesos.
- https://www.urionlinejudge.com.br/judge/pt/problems/view/1907 - Contagem de componentes conexas em grafo que é um grid (implícito).
- https://codeforces.com/gym/102346/problem/A - Se considerarmos as paredes e sensores vértices, vendo se alguns vértices estão na mesma componente conexa podemos ver se há um caminho que bloqueia o ladrão.
- https://www.urionlinejudge.com.br/judge/pt/problems/view/2194 - (implementação mais difícil), resolver o reconhecimento por meio da contagem das componentes conexas de cada hieróglifo.
Busca em Largura
Podemos chamá-la também de BFS (Breadth-First Search).
Uma das formas de percorrer um grafo é fazer um percorrimento em largura. Começamos a explorar os vértices do grafo a partir de um certo vértice a. E a ordem que vamos navegando entre os vértices é de forma que os mais próximos a a sempre serão visitados antes. Então, primeiro a será visitado, depois os vértices que são adjacentes a a(distância 1), depois os vértices que estão a duas arestas de distância, e assim por diante. Como os vértices mais próximos são sempre visitados antes, esse algoritmo serve para, por exemplo, dizer qual a distância mínima entre dois vértices no grafo.
Esse comportamento é implementado usando-se uma fila. Primeiro insere-se na fila o vértice inicial, e começa-se a desenfileirar da fila enquando houver algum nodo. Quando um vértice a é desenfileirado, enfileram-se todos os vértice adjacentes a a que não foram visitados. Caso não marquemos os visitados, e o grafo tiver ciclos, nosso programa não terminará.

O algoritmo abaixo é uma BFS que simplesmente percorre o grafo.
const int MAX_SIZE = 1e5;
// globais
// inicializa visited como false
bool visited[MAX_SIZE];
vector<int> graph[MAX_SIZE];
void bfs(int start){
queue<int> q;
q.push(start);
visited[start] = true;
while(!q.empty()){//Enquanto não estiver vazia
// Retire o vértice da frente
int u = q.front();
q.pop();
for(int w: graph[u]){ // Para cada vértice adjacente a u
if(!visited[w]){
q.push(w);
visited[w] = true;
}
}
}
}
A complexidade desse código é O(n+m), temos no máximo n vértices enfileirados, e no loop interno, cada iteração é considerar uma aresta, como não estamos voltando no grafo, não passaremos por uma aresta mais que duas vezes naquele loop. Então, em todas as chamadas, aquele loop iterará no pior caso m vezes.
Busca em Profundidade
Outra forma de percorrer um grafo é fazer percorrimento em profundidade, também de chamado de DFS(Depth-first search). O algoritmo se chama assim porque funciona de uma forma que sempre vamos ‘mergulhar’ no grafo o mais fundo que pudermos. Quando não for mais possível ir mais fundo no grafo, voltamos até que seja ir mais fundo novamente, sem repetir vértices já visitados.
A implementação da DFS mais comum é recursiva, por ser mais intuitiva. Assim como o exemplo anterior, esse programa simplesmente percorre o grafo, mas na ordem que um DFS percorre.
Visualização

Implementação
const int MAX_SIZE = 1e5;
vector<int> graph[MAX_SIZE];
bool visited[MAX_SIZE]; // globais, inicializados na main.
void dfs(int vertex){ // na main chamamos dfs(start), aonde start é o vértice que começamos o dfs
visited[vertex] = true;
for(int w: graph[vertex]){
if(!visited[w]){
dfs(w);
}
}
}
A complexidade desse código é O(n+m), temos no máximo n chamadas recursivas, e no loop interno às chamadas, assim como no BFS, estaremos considerando uma aresta e não passaremos nela mais de uma vez. Então no máximo m iterações ao longo de todas as chamadas.
Dijkstra
O(E*log(V))
E = Edges
V = Vertex
O algoritmo de Dijkstra é um algoritmo muito conhecido para percorrimento de grafos cujas arestas tem pesos, ele nos permite percorrer os vértices na ordem de distância para um vértice fonte. E efetivamente descobrir essas distâncias.
Mais especificamente, de uma forma tal que considerando o vértice fonte como s, se o menor caminho de s para um vértice u é estritamente menor que o menor caminho de s para um outro vértice v, com certeza visitaremos u antes de v.
A forma como o algoritmo opera é muito parecida com o BFS, mas em vez de usarmos uma fila, usamos uma fila de prioridades(priorizando menores valores). O motivo de usarmos essa outra estrutura de dados é que usar uma fila não gera mais o mesmo comportamento que desejamos quando as arestas passam a ter pesos.
Como as arestas tem pesos, nosso grafo será um vector<pair<int,int>> grafo[n] ao invés de um vector<int> grafo[n].
A ideia
Assim como no BFS, teremos essa fila que ditará a ordem com que os nodos serão desenfileirados (visitados). Mas agora Nossa Fila é de prioridades abriga pares ao invés de apenas um inteiro.
Pra qualquer par p na fila, (p.first,p.second) significa: Consigo chegar no vértice p.second por um caminho de custo p.first. Por isso no começo da execução enfileiramos o par (0, s), dizendo: consigo chegar no vértice fonte pagando 0, afinal já estamos nele no começo do percorrimento.
Quando desinfileiramos um vértice, assim como no BFS, consideramos seguir por todas as arestas que partem dele, agora com pesos.
Bem, para cada aresta, sabemos seu destino e seu peso, então, a informação que podemos tirar disso é que podemos ir para aquele destino com o custo da aresta somado com o custo para chegar no vértice que acabamos de desinfileirar.
Na implementação do BFS, na hora de verificar se devíamos enfileirar algo, verificavamos apenas se aquele destino já tinha sido enfileirado antes, usando um vetor pra armazenar essa informação.
Na nossa implementação, ao invés de um vetor marcando quais já foram enfileirados, usaremos um vetor indicando o melhor custo conhecido para se atingir cada vértice.
O motivo disso é que não há mais garantia que na primeira vez que enfileiramos um vértice já obtivemos o melhor custo para chegar nele. Pode ser que posteriormente enfileiremos um custo menor pra chegar nesse vértice.
Então, na hora de enfileirarmos, verificaremos se aquele enfileiramento é vantajoso, isto é, se ele melhora o melhor custo que já conhecíamos para chegar em algum vértice. De começo assumimos o custo infinito para chegar em todos.
Visualização

Implementação
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100005;
const ll oo = 1e18;
ll d[N]; // vetor onde guardamos as distancias
int n; // numeros de vertices
// lista de adjacencias guarda
// pair <vertice para onde a aresta vai, peso da aresta>
vector<pair<int, ll>> g[N];
void dijkstra(int start){
// inicialmente a distancia do vertice
// start para todo os outros é infinita
for(int u = 1; u <= n; u++)
d[u] = oo;
// fila de prioridade de pair<ll, int>, mas que o
// menor pair fica no topo da fila
// guardamos um pair <distancia ate o vertice, vertice>
// assim o topo da fila sempre é o vertice com menor distancia
priority_queue<pair<ll, int>, vector<pair<ll, int>>,
greater<pair<ll, int>> > pq;
d[start] = 0;
pq.emplace(d[start], start);
ll dt, w;
int u, v;
while(!pq.empty()){
tie(dt, u) = pq.top(); pq.pop();
if(dt > d[u]) continue;
for(auto edge : g[u]){
tie(v, w) = edge;
// se a distancia ate o u somado com o peso
// da aresta é menor do que a distancia ate o v que
// tinhamos antes, melhoramos a distancia ate o v
if(d[v] > d[u] + w){
d[v] = d[u] + w;
pq.emplace(d[v], v);
}
}
}
}
int main(){
// lê o input, qnt de vertices, arestas
// e vertice inicial(start)
dijkstra(start);
for(int u = 1; u <= n; u++){
printf("Distancia de %d para %d: %lld\n", start, u, d[u]);
}
}
Assim como no BFS, podemos facilmente adicionar um vetor indicando os predecessores de cada vértice, dessa forma podemos obter não só a informação dos custos, mas também a sequência de vértices que a origina.
Bitwise
Representação binária
Qualquer tipo de dado, seja um número inteiro, número racional ou um caracter, pode ser representado por bits.
Exemplos de representação binária de números inteiros (sem sinal):
1) 14 = {1110}2 = 1 * 2^3 + 1 * 2^2 + 1 * 2^1 + 0 * 2^0 = 14.
2) 20 = {10100}2 = 1 * 2^4 + 0 * 2^3 + 1 * 2^2 + 0 * 2^1 + 0 * 2^0 = 20.
Operadores bit-a-bit
NOT ( ~ ): Bitwise NOT é um operador unário que flipa os bits de um número (se o bit é 0, vira 1 e vice-versa). Bitwise NOT é apenas o complemento de 1 de um número.
N = 5 = (101)2
~N = ~5 = ~(101)2 = (010)2 = 2
AND ( & ): Bitwise AND é um operador binário que opera em duas palavras de bits de mesmo tamanho. Se ambos os bits na posição comparada das palavras forem 1, então o valor do bit resultante nessa posição na palavra final será 1, qualquer outro caso o bit resultante será 0.
A = 5 = (101)2
B = 3 = (011)2
A & B = (101)2 & (011)2= (001)2 = 1
OR ( | ): Bitwise OR, similarmente ao bitwise AND, é um operador binário que opera em duas palavras de bits de mesmo tamanho. Se ambos os bits na posição comparada forem 0, o valor do bit resultante nessa posição na palavra final será 0, qualquer outro caso o bit resultante será 1.
A = 5 = (101)2
B = 3 = (011)2
A | B = (101)2 | (011)2 = (111)2 = 7
XOR ( ^ ): Bitwise XOR também é um operador binário que opera em duas palavras de bits de mesmo tamanho. Se ambos os bits na posição comparada forem iguais (0 ou 1), o valor do bit resultante nessa posição na palavra final será 0, se os bits forem diferentes (um 0 e outro 1), o bit resultante será 1.
A = 5 = (101)2
B = 3 = (011)2
A ^ B = (101)2 ^ (011)2 = (110)2 = 6
Left Shift ( « ): Existem dois operadores de deslocamento (left shift e righr shift). O left shift operator é um operador binário que desloca os bits de uma palavra X vezes para a esquerda e preenche a palavra com X 0s à direita. Left shift de X bits em um número inteiro é equivalente a multuplicá-lo por 2^X.
1 « 1 = 2
1 « 2 = 4
2 « 2 = {00010}2 « 2 = {01000}2 = 8
1 « n = 2^n
Right Shift ( » ): O right shift operator é um operador binário que desloca os bits de uma palavra X vezes para a direita e preenche a palavra com X 0s à esquerda. Right shift de X bits em um número inteiro é equivalente a dividi-lo por 2^X.
4 » 1 = 2
6 » 1 = 3
5 » 1 = 2
16 » 4 = 1
Tabela-verdade
| X | Y | X&Y | X|Y | X^Y |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Manipulando bits
Checando se um determinado bit está ligado
Para checarmos de um jeito eficiente se o i-ésimo bit de um número N está ligado, basta apenas checar se o AND de 2^i e N é diferente de 0. Como vimos anteriormente, o número 2^i é simplesmente o número 1 shiftado de i bits (1 « i).
bool isSet(int bitPosition, int number) {
bool ret = ((number & (1 << bitPosition)) != 0);
return ret;
}
Ligando um determinado bit em um número
Para ligar o i-ésimo bit de um número N, basta apenas fazermos o OR de 2^i com N.
bool setBit(int bitPosition, int number) {
return (number | (1 << bitPosition) );
}
Representando conjunto com bits - bitmasks
Suponha que tenhamos conjunto universo com 8 elementos, U = {a,b,c,d,e,f,g,h}.
Vamos associar cada elemento de U a um bit:
a -> bit 7
b -> bit 6
c -> bit 5
d -> bit 4
e -> bit 3
f -> bit 2
g -> bit 1
h -> bit 0
Com essa associação, podemos representar qualquer subconjunto de U como uma máscara de 8 bits. Exemplo:
| Conjunto | Bitmask |
|---|---|
| {b,c,f,h} | 01100101 |
| {a} | 10000000 |
| {} | 00000000 |
Adicionar um elemento ao conjunto
Para adicionarmos um elemento a um conjunto que está representado como uma bitmask é simples. Basta apenas setarmos o bit correspondente ao elemento na bitmask do conjunto.
int addElement(int bitmask, int elementPosition) {
bitmask = bitmsak | (1 << elementPosition);
return bitmask;
}
Checar se um conjunto contem um elemento
Essa operação é a mesma de checar se um dado bit está setado na bitmask.
bool hasElement(int bitmask, int elementPosition){
bool ret = ((bitmask & (1 << elementPosition)) != 0);
return ret;
}
União de 2 conjuntos
Um elemento estará presente na união de 2 conjuntos se e somente se pelo menos um dos conjuntos contiver este elemento. Com base nisso e na tabela-verdade, podemos ver que a máscara que representa a união de duas máscaras é o OR delas.
int union(int bitmaskA, int bitmaskB){
return (bitmaskA | bitmaskB);
}
Interseção de 2 conjuntos
Um elemento estará presente na interseção de 2 conjuntos se e somente se os 2 conjuntos contiverem este elemento. Logo, a máscara que representa a interseção de duas máscaras é o AND delas.
int intersection(int bitmaskA, int bitmaskB){
return (bitmaskA & bitmaskB);
}
Gerando todos os subconjuntos de um conjunto
Suponha que você tenha um conjunto S = {p,q,r}.
Para formar um subconjunto de S, podemos escolher ou não o elemento p (2 opções), escolher ou não o elemento q (2 opções de novo) e escolher ou não o elemento r (2 opções novamente). Logo, podemos formar um subconjunto de S de 2*2*2 maneiras diferentes.
Um conjunto de N elementos possui 2^N subconjuntos. S possui 2^3 = 8 subconjuntos.
Ok, agora vamos representar cada elemento do conjunto S com um bit, como S tem 3 elementos, precisamos de 3 bits para isso:
p = bit 2,
q = bit 1,
r = bit 0
Com esta associação de elementos e bits, podemos representar todos os subconjuntos de S como uma palavra de 3 bits. Veja:
0 = (000)2 = {}
1 = (001)2 = {r}
2 = (010)2 = {q}
3 = (011)2 = {q, r}
4 = (100)2 = {p}
5 = (101)2 = {p, r}
6 = (110)2 = {p, q}
7 = (111)2 = {p, q, r}
Como temos 2^N subconjuntos em um conjunto de N elementos, passando por todos os números de [0, 2^N - 1] é possível representar todos os subconjuntos de um conjunto.
Código para printar todos os subconjuntos de um conjunto:
void possibleSubsets(char S[], int N) {
for(int i = 0;i < (1 << N); ++i) { // i = [0, 2^N - 1]
for(int j = 0;j < N;++j)
if(i & (1 << j)) // se o j-ésimo bit de i está setado, printamos S[j]
cout << S[j] << " ";
cout << endl;
}
}
Matematica
Subpáginas
Subsecções de Matematica
Módulo
Diversos problemas em juízes online (e competições) costumam pedir a resposta módulo algum primo alto (bastante comum 10^9 + 7). O motivo disso é evitar overflow. Por exemplo: finja que você tem o seguinte problema:
Imprimir o resultado de 3^x (0 <= x <= 100), por exemplo. Esse resultado claramente excede 2^64 (limite de long long), então não faz muito sentido pedir o resultado por si só (na verdade, alguns problemas realmente pedem coisas do tipo, nesses casos, o recomendado é usar python, que não tem overflow).
Então pedem o resultado módulo 10^9 + 7, ou algum primo muito alto, para que não force as pessoas a usarem uma linguagem ou outra.
O motivo de ser um número alto é minimizar a chance de seu programa a computar a resposta errada (e por sorte ser igual em módulo a resposta correta) e o juíz aceitá-la.
O motivo de ser um número primo é que adicionam algumas propriedades a mais que podemos usar para calcular a resposta, como o inverso multiplicativo, mas não abordaremos isso aqui.
As seguintes propriedades valem no cálculo do módulo:
(a + b) % c = ((a % c) + (b % c)) % c
(a * b) % c = ((a % c) * (b % c)) % c
O que isso quer dizer é que se a resposta está sendo computada por meio de adições e multiplicações, e no final você precisa tirar o módulo dela, você pode tirar módulo em todas as operações intermediárias que isso não afetará a resposta.
Então, por exemplo:
long long exp(int p) {
if(p == 0)
return 1;
return 3ll * exp(p-1);
}
int main() {
int mod = 1e9+7;
int n;
scanf("%d",&n);
printf("%lld\n", exp(n) % mod);
}
O código acima gera overflow, a resposta vai estourar o limite de long long (já terá se tornado negativa) quando tirarmos o mod. No entanto, conceitualmente, ele está correto.
Então, usando as propriedades vistas em cima, podemos fazer:
int mod = 1e9+7;
long long exp(int p) {
if(p == 0)
return 1;
return (3ll * exp(p-1)) % mod;
}
int main() {
int n;
scanf("%d",&n);
printf("%lld\n", exp(n));
}
De forma que o código acima imprime (3^n) % (1000000007), sem causar overflow.
Divisores
Um problema recorrente é o de encontrar divisores de um número positivo. A maneira mais simples de resolvê-lo seria passar por todos os números e testar se o resto da divisão é 0, ou seja, se é divisível.
vector<long long> all_divisors(long long n) {
vector<long long> ans;
for(long long i = 1; i <= n; i++)
if(n % i == 0)
ans.push_back(i);
return ans;
}
é fácil ver que a complexidade do código acima é O(n), podemos fazer melhor que isso com algumas observações.
Se a é um divisor n então o resto da divisão de n por a é 0 assim b = n/a é um inteiro. Sabemos então que a*b = n, ou seja, a = n/b e assim b também é um divisor de n. Se fixarmos que a <= b, qual o valor máximo de a? Como a é no máximo b, consideremos o caso em que a = b temos que a*a = n, ou seja, a = sqrt(n).
Agora é possivel modificar o código passando por todos os valores possíveis de a e computar o respectivo b para encontrar todos os divisores.
vector<long long> all_divisors(long long n) {
vector<long long> ans;
for(long long a = 1; a*a <= n; a++) { // comparação que evita o uso de doubles, a <= sqrt(n) é o mesmo que a*a <= n, ja que a e n sao positivos
if(n % a == 0) {
long long b = n / a;
ans.push_back(a);
ans.push_back(b);
}
}
sort(ans.begin(), ans.end()); // frescura para retornar os divisores ordenados como na primeira implementação
return ans;
}
Só há um problema com a implementação acima. Assumimos que a <= b, caso a = b inserimos o divisor 2 vezes na resposta, por exemplo, para 36 podemos ter a = 6 e b = 6. Assim a versão final do código fica:
vector<long long> all_divisors(long long n) {
vector<long long> ans;
for(long long a = 1; a*a <= n; a++) { // comparação que evita o uso de doubles, a <= sqrt(n) é o mesmo que a*a <= n
if(n % a == 0) {
long long b = n / a;
ans.push_back(a);
if(a != b) ans.push_back(b);
}
}
sort(ans.begin(), ans.end()); // frescura para retornar os divisores ordenados como na primeira implementação
return ans;
}
com complexidade O(sqrt(n)).
Observações
Um número primo tem somente dois divisores positivos, assim podemos checar se um numero x é primo usando all_divisors(x).size() == 2 ou modificando um pouco a rotina e ter uma melhor constante na complexidade
vector<long long> is_prime(long long n) {
if(n == 1) return 0;
for(long long a = 2; a*a <= n; a++) { // comparação que evita o uso de doubles, a <= sqrt(n) é o mesmo que a*a <= n
if(n % a == 0){
return 0;
}
}
return 1;
}
Passar por todos os múltiplos de x até N
Consideramos multiplos de x os números: x, 2*x, 3*x, 4*x, ... ou, escrevendo de outra forma, x, x+x, x+x+x, x+x+x+x, ...
Caso queiramos fazer algo com todos os múltiplos de x até um limite N podemos usar a simples rotina
for(int m = x; m < N; m += x) { // m é sempre multiplo de x
// code
}
Que é executada em O(N/x).
Passar por todos os múltiplos de todos os números até N
Se passarmos por todos os números x entre 1 e N e para cada um deles achar todos os múltiplos m.
O código ficaria algo como
for(int x = 1; x < N; x++) {
for(int m = x; m < N; m += x) { // m é sempre multiplo de x
// code
}
}
O código acima parece ser executado em O(N^2), mas podemos definir uma cota bem menor, com algumas observações. O código é executado em N/1 + N/2 + ... + N/(N-1) + N/N passos. Podemos botar o N em evidencia N*(1/1 + 1/2 + 1/3 + ... + 1/(N-1) + 1/N). A soma dentro dos parenteses é menor que a área abaixo da curva da função 1/x, a integral é ln(x)(mas relaxa que não precisa lembrar das coisas de cálculo 1). Portanto O(N*(1/1 + 1/2 + 1/3 + ... + 1/(N-1) + 1/N)) = O(N*lg N).
Podemos resolver vários problemas usando isso pois x será divisor de m e assim para todo m também passaremos por todos os divisores deles.
Contando os divisores de vários números
Por exemplo, usando essa abordagem, poderíamos usar esses 2 laços aninhados para gerar um vetor div que informa quantos divisores todos os números até n tem.
Perceba que esses dois laços executam em O(n * log n), enquanto repetir o algoritmo de contar os divisores de cada número individualmente teria complexidade sqrt(1) + sqrt(2) + ... + sqrt(n) = O(n * sqrt(n)), ou seja, tem complexidade melhor.
A abordagem abaixo funciona porque sempre que chegamos em um número m no laço mais interno, significa que temos um divisor a mais.
Na primeira iteração passamos por todos os números, já que começamos e 1 e estamos incrementando de 1 em 1, todos os números são divisíveis por 1, então todos ganham um divisor a mais no vetor.
Na segunda iteração, passamos apenas pelos números múltiplos de 2, em todos os números que chegarmos, significa que esse número é divisível por 2 (ou seja, sabemos que ele tem um divisor a mais). E repetimos esse raciocínio para todos os números.
vector<int> computa_divisores(int N) {
vector<int> qnt_div(N, 0);
for(int x = 1; x < N; x++) {
for(int m = x; m < N; m += x) {
qnt_div[m]++; // aqui descobrimos que x é divisor de m
}
}
return qnt_div;
}
Números Primos
Em particular, sabendo a quantidade de divisores de cada número, podemos varrer esse vetor vendo quais números são primos (tem 2 divisores).
vector<int> primos_ate_n(int N) {
vector<int> primos;
for(int x = 1; x < N; x++) {
if(qnt_div[x] == 2)
primos.push_back(x);
}
return primos;
}
Crivo de erastótenes
A abordagem acima tem uma complexidade aceitável, e passaria no tempo para a maioria dos problemas. No entanto, existe um algoritmo com uma ideia semelhante, mas que com algumas observações baixa essa complexidade de O(n * log n) para O(n * log( log n)). O log já abaixa muito um número, se aplicamos ele novamente, abaixamos mais ainda, ou seja, isso é quase linear.
A ideia usada é marcar inicialmente todos os números entre 1 e N como possiveis primos. Passando em ordem crescente e quando encontramos um primo marcamos os múltiplos do primo como não primos.
Visualização

Implementação
vector<int> primos_ate_n(int N) {
vector<int> marcacao(N, 1); // 1 = possivel primo, 0 = com certeza não primo
vector<int> primos;
for(int x = 2; x < N; x++) if(marcacao[x] == 1) {
primos.push_back(x);
for(int m = x+x; m < N; m += x) {
marcacao[m] = 0; // aqui descobrimos que m não é primo
}
}
return primos;
}
Fatoração
Aprendemos na escola que todo número é composto por fatores primos, existindo uma única fatoração pra cada número.
Uma primeira abordagem possível seria passar por todos os números e ir dividindo sempre que possível.
// retorna vetor de pair<primo, expoente> da fatoração
// fatora(36) = [{2, 2}, {3, 2}] ou seja, 36 = 2^2 + 3^2
vector<pair<long long, int>> fatora(long long n) {
vector<pair<long long, int>> ans;
for(long long p = 2; p <= n; p++) {
if(n % p == 0){
int expoente = 0;
while(n % p == 0) {
n /= p;
expoente++;
}
ans.emplace_back(p, expoente);
}
}
return ans;
}
A primeira vista,como queremos decompor em fatores primos, parece que temos que testar se p é primo. Entretanto passamos por p de forma crescente e sempre que podemos dividimos n por p então a condição (n % p == 0) só será verdade para p primos.
Isso ocorre porque todos os fatores primos de um número são menores ou iguais a ele próprio, então quando chegamos em um número, é impossível que ele divida o número e não seja primo, pois se não for, os números primos que o compoem deveriam ter sido contabilizados numa iteração anterior.
Apesar do código acima rodar bem para vários exemplos, no pior caso n é primo e o código é executado em O(n).
Podemos melhorar a complexidade com uma simples observação. É possivel ter apenas um primo maior que a sqrt(n), por exemplo, 10 tem 5 como fator e 5 > sqrt(10), mas é impossível ter dois primos maiores que a raiz. Se tivermos a > sqrt(n) e b > sqrt(n), quando multiplicamos temos que a * b > sqrt(n) * sqrt(n) e a * b > n.
vector<pair<long long, int>> fatora(long long n) {
vector<pair<long long, int>> ans;
for(long long p = 2; p*p <= n; p++) { // comparação que evita o uso de doubles, p <= sqrt(n) é o mesmo que p*p <= n
if(n % p == 0) {
int expoente = 0;
while(n % p == 0) {
n /= p;
expoente++;
}
ans.emplace_back(p, expoente);
}
}
if(n > 1) ans.emplace_back(n, 1);
return ans;
}
Fatoração em O(lg n) para números até N
É possível fatorar números ate um limite N em O(lg n) após preprocessamento O(n log( log n)). O que fazemos é uma pequena modificação no código do crivo, para que enquanto fazemos o crivo, preenchamos um vetor auxiliar lp, aonde lp[x] representa o maior número primo que divide x.
vector<int> lp(N, -1);
for(int x = 2; x < N; x++)
if(lp[x] == -1) { // se x nao foi marcado antes, é primo
for(int m = x; m < N; m += x) // todos os multiplos de i
lp[m] = x;
}
Tendo este vetor podemos fatorar um numero x com o seguinte procedimento.
vector<pair<int, int>> fatora(int x) {
map<int, int> expoentes;
while(x > 1) {
expoentes[ lp[x] ]++; // aumentamos o expoente do primo lp[x] em 1 na resposta
x /= lp[x];
}
vector<pair<int, int>> ans;
for(pair<int, int> p : expoentes)
ans.emplace_back(p);
return ans;
}
A complexidade do procedimento acima é O(quantidade de fatores), que é limitado por O(lg n), da para ver que no pior caso todos os fatores são 2(menor primo) e a complexidade é o k de 2^k = n.
Número de divisores dada uma fatoração
Vimos que todo inteiro N pode ser escrito de forma única como multiplicação de números primos. Assim,
$$N = {p_1}^{e_1}.{p_2}^{e_2}.{p_3}^{e_3}.{p_4}^{e_4}.{p_5}^{e_5}.{p_6}^{e_6} ... $$onde pi é primo e 0 ei > 0.
Todo divisor de N só pode ter primos que aparecem na fatoração de N e expoente no máximo o do expoente no N. Por exemplo: $$36 = 2^2.3^2$$
$$1 = 2^0.3^0$$ $$2 = 2^1.3^0$$ $$3 = 2^0.3^1$$ $$4 = 2^2.3^0$$ $$6 = 2^1.3^1$$ $$9 = 2^0.3^2$$ $$12 = 2^2.3^1$$ $$18 = 2^1.3^2$$ $$36 = 2^2.3^2$$Para construir um divisor podemos escolher dentre (ei+1) possibilidades para o primo pi. O número total de divisores é a multiplicação desses termos. Assim 36 tem (2+1)*(2+1) = 9 divisores.
Embora esta ideia não melhore a complexidade para encontrar o número de divisores em comparação com as ideias anteriores, ela pode ser uma ferramenta útil para analisar problemas. Por exemplo, os números com exatamente 9 divisores são da forma
$${p_1}^8={p_1}^2.{p_2}^2$$Como por exemplo:
$$256 = 2^8$$ $$6561 = 3^8$$ $$36 = 2^2.3^2$$ $$100 = 2^2.5^2$$ $$255 = 3^2.5^2$$etc…
Tópicos Avançados
Subpáginas
Subsecções de Tópicos Avançados
Lowest Common Ancestor
Lowest Common ancestor (LCA) - ou ancestral comum mais baixo, é o nome típico dado para o seguinte problema: dado uma Árvore cuja raiz é um vértice arbitrário e dois vértices u,v que a pertencem, diga qual é o nó mais baixo(relativo a raiz) que é ancestral de u,v.

Por exemplo na imagem a cima, o LCA de 2 e 3 é 1, o LCA de 6 e 7 é 0, e o LCA de 1 e 2 é 1.
um jeito naive de se fazer isso seria o seguinte, para cada nó da árvore, pré-processamos sua profundidade com relação a raiz (raiz tem profundidade 0, filhos 1, e assim por diante). Agora, para determinarmos os LCA de dois vértices u,v, podemos fazer o seguinte procedimento. Escolhemos qual dos dois vértices está mais profundo, subimos nos seus pais até igualar as alturas de ambos, e após isso, vamos subindo em ambos os caminhos um a um até que os caminhos se encontrem, então saberemos o LCA.
int depth[100005];
vector<int> graph[100005];
void pre_process_depth(int u, int d) {
depth[u] = d;
for(auto adj : graph[u]) {
pre_process_depth(adj, d + 1);
}
}
int slow_lca(int u, int v) {
if(depth[u] < depth[v]) {
swap(u, v);
}
while(depth[u] > depth[v]) {
u = pai[u];
}
while(u != v) {
u = pai[u];
v = pai[v];
}
return u;
}
Essa estratégia efetivamente funciona, então teríamos um pré-processamento que é um DFS e após isso conseguiríamos responder queries em O(n), pois numa árvore com um ramo muito profundo teríamos no pior caso que subir todos os vértices, portando complexidade total de O(n + Qn) = O(Qn) onde Q é o número de queries e n a quantidade de nós na árvore.
O LCA é relevante porque como em uma árvore há um único caminho que liga dois vértices, se conseguimos obter o LCA rápido então uma das coisas que já ganhamos de quebra é conseguir responder as distâncias entre quaisquer par de vértices.
A distância vai ser a distância de um vértice para o LCA e do LCA para o outro, sendo que essas duas distâncias intermediárias são apenas a diferença de alturas na árvore.
Aqui nesse tutorial vamos mostrar duas ideias para computar LCA, uma que vai nos permitir responder Queries de LCA em O(log n) com preprocessamento O(n log n) e uma segunda abordagem que vai nos permitir responder queries de LCA em O(1) (isso mesmo, tempo constante!) com preprocessamento O(n log n) também.
Apesar de a complexidade da segunda abordagem para responder queries de LCA ser estritamente melhor que da primeira, veremos que a primeira carrega um pouco mais de informação, permitindo obter algumas outras informações fora o LCA, enquanto na segunda podemos obter apenas o LCA.
Abordagem 1
O problema da solução naive é essa subida de um em um até que atinjamos o pai comum. Então faz sentido tentarmos atacarmos isso para ganhar um desempenho assintótico melhor. Uma coisa a se observar é que estamos fazendo duas buscas lineares. A primeira busca linear é pelo primeiro ancestral de u que iguala a altura a v e após isso outra busca linear para procurar o primeiro ancestral de ambos que é comum.
Podemos observar que há monotonicidade nessas buscas lineares, até certo ponto os ancestrais não satisfazem uma condição, e após certo ponto todos satisfazem. Na primeira estaríamos buscando o ancestral mais baixo de u que satisfaz a condição “Ter altura menor ou igual a v”, e na segunda “Ser ancestral de v”.
Aqui usaremos o conceito de “k-ésimo pai” que funciona assim: o primeiro pai é o pai do vértice, o segundo pai é o pai do pai do vértice, e assim por diante.
Se nós tivéssemos uma função mágica chamada por exemplo climb(n,k) que nos retornasse o k-ésimo pai do vértice n, poderíamos então usar buscas binárias na quantidade de vértices a subir para resolver esse problema, e restaria implementar essa função de maneira eficiente. Vamos seguir por essa linha de raciocínio então.
O pulo do gato
Se nós tivéssemos uma outra função mágica chamada p2k(n,k) que retorna o (2^k)-ésimo pai de um vértice n, poderíamos implementar a função que sobe k vértices da seguinte maneira. Se nosso grafo tem tamanho menor que 10^6, sabemos que não precisamos subir mais do que 2^20.
int climb(int node, int k){
for(int i = 20; i >= 0; i--) {
if(k >= (1 << i)) {
node = p2k(node,i);
k -= (1 << i);
}
}
return node;
}
A complexidade dessa função depende do número que colocamos no for, que não precisa ser maior do que o log do tamanho do grafo(não faz sentido subir mais nós do que o grafo possui), então conseguimos obter o k-ésimo ancestral de um vértice arbitrário em complexidade O(log) * X aonde X é a complexidade de p2k.
Mostramos agora que podemos preprocessar todos os valores possíveis de p2k em O(n log n). Precisamos saber os valores dos ancestrais para todos os n vértices e para cada vértice só faz sentido saber log ancestrais. Podemos obter todos os valores de uma vez usando programação dinâmica, com uma recorrência muito elegante.
int p2k(int node, int k) {
if(k == 0) {
return pai[node];
}
return p2k(p2k(node, k-1),k-1);
}
Versão recursiva
Usamos então memoização para computarmos cada estado em O(1)
int memo[SIZE][log2(GRAPHSIZE)];
int p2k(int node, int k) {
if(k == 0) {
return pai[node];
}
if(memo[node][k] != -1) {
return memo[node][k];
}
return memo[node][k] = p2k(p2k(node, k-1),k-1);
}
Versão iterativa
int p2k[SIZE][log2(SIZE)+1];
for(int node = 0; node < SIZE; node++) {
p2k[node][0] = pai[node];
}
for(int k = 1; k <= log2(SIZE); k++) {
for(int node = 0; node < SIZE; node++) {
p2k[node][k] = p2k[p2k[node][k-1]][k-1];
}
}
Dessa forma então temos o seguinte procedimento para acharmos o LCA, fazemos uma busca binária, em cada iteração obtemos o k-ésimo ancestral, e checamos se ele satisfaz as propriedades, tendo então complexidade O(log n * log n) = O(log^2 n), já que fazemos log iterações e em cada iteração demoramos log para obter o k-ésimo ancestral. Isso funciona, mas podemos melhorar um pouco mais.
Ao invés de usarmos busca binária vamos usar uma técnica conhecida como binary lifting ou escalada binária, basicamente vamos percorrer bit a bit vendo se esse bit está na resposta ou não.
A ideia é a seguinte, vamos supor que a resposta da busca binária de o quanto eu tenho que subir a partir de um vértice para satisfazer uma propriedade seja 6(o primeiro ancestral que satisfaz a propriedade é o sexto pai). Podemos usar escala binária para procurar pelo último vértice que ainda não satisfaz a propriedade (no caso então seria o 5).
Usando nossa função p2k, podemos começar vendo se o oitavo pai já satisfaz a propriedade e sim satisfaz, então como estamos buscando o último que ainda satisfaz, não subimos para o oitavo pai. Depois verificamos que o quarto pai que ainda não satisfaz, então subimos para ele. Depois verificamos o segundo pai do quarto pai, isto é, o sexto pai do vértice original, que já satisfaz, então não subimos para ele, e por último, verificamos o pai do quarto pai (quinto pai do vértice original), que não satisfaz, então subimos pra ele e sabemos o último vértice que ainda não satisfaz a propriedade.
A escalada binária pode ser usada nas mesmas situações aonde a busca binária pode ser usada, mas algumas vezes (como essa), podemos obter uma complexidades assintóticas melhores.
Cada checagem para ver se um dos (2^k)-ésimos pais satisfazem a propriedade é constante, e checamos os pais (2^k), 2^(k-1), 2^(k-2),..., 1 sempre dividindo por 2, então passamos por no máximo log vezes nessa checagem, portanto com essa ideia podemos obter o lca em O(log n).
int lca(int u, int v) {
if(depth[u] < depth[v]) swap(u,v);
for (int i = 20; i >= 0; --i) {
if(depth[p2k[u][i]] >= depth[v])
u = p2k[u][i];
}
if(u == v) return u;
for (int i = 20; i >= 0; --i) {
if(p2k[v][i] != p2k[u][i]) {
v = p2k[v][i];
u = p2k[u][i];
}
}
return pai[v];
}
Perceba que estamos fazendo exatamente a ideia primeiramente apresentada na solução naive. Primeiro pegamos o vértice que está mais embaixo e subimos ele até o nível do outro, e após isso, subimos em ambos os vértices procurando o primeiro ancestral comum, mas em vez de fazermos busca linear, fazemos escalada binária.
A escala binária desempenha melhor nessa situação(em relação a busca binária) porque quando vamos construir o (n-ésimo) pai para fazer a checagem (somando vários (2^k)-ésimos pais) na busca binária, estaríamos colocando os mesmos vértices todas as vezes, por exemplo, tome o exemplo aonde o último vértice que satisfaz uma propridade é o 26.
l = 0, r = 32, mid = 16(16), checagem passa.
l = 16, r = 32, mid = 24(16 + 8), checagem passa.
l = 24, r = 32, mid = 28(16 + 8 + 4), checagem falha
l = 24, r = 28, mid = 26(16 + 8 + 2), checagem passa
l = 26, r = 28, mid = 27(16 + 8 + 2 + 1), checagem falha
Quando a checagem passou para mid = 16, podíamos ter certeza que tinhamos que subir pelo menos até o décimo sexto pai, mas aí nos checks subsequentes perdemos tempo reconstruindo a resposta que já conhecemos. Então o que a escala binária faz é tomar vantagem disso.
Versão final do código
Agora como mencionado podemos obter rapidamente a distância entre quaisquer 2 nós na árvore.
int dist(int u, int v){
return depth[u] + depth[v] -2*depth[lca(u,v)];
}
Versão final do código
Apesar de não fazermos a busca binária que usava a função climb no final, é possível que essa implementação seja útil em alguns problemas.
int depth[SIZE];
vector<int> graph[SIZE];
void pre_process_depth(int u, int d) {
depth[u] = d;
for(auto adj : graph[u]) {
pre_process_depth(adj, d + 1);
}
}
int p2k[SIZE][log2(SIZE)+1];
int lca(int u, int v) {
if(depth[u] < depth[v]) swap(u,v);
for (int i = 20; i >= 0; --i) {
if(depth[p2k[u][i]] >= depth[v])
u = p2k[u][i];
}
if(u == v) return u;
for (int i = 20; i >= 0; --i) {
if(p2k[v][i] != p2k[u][i]) {
v = p2k[v][i];
u = p2k[u][i];
}
}
return pai[v];
}
int climb(int node, int k){
for(int i = 20; i >= 0; i--) {
if(k >= (1 << i)) {
node = p2k[node][i];
k -= (1 << i);
}
}
return node;
}
int dist(int u, int v){
return depth[u] + depth[v] -2*depth[lca(u,v)];
}
int main() {
// codigo
// le os pais e monta o grafo
pai[raiz] = raiz;
pre_proccess_depth(raiz); // tipicamente qual vertice é a raiz nao importa
for(int node = 0; node < SIZE; node++){
p2k[node][0] = pai[node];
}
for(int node = 0; node < SIZE; node++) {
for(int k = 1; k <= log2(SIZE); k++) {
p2k[node][k] = p2k[p2k[node][k-1]][k-1];
}
}
// resolve problema
}
Conclusão
Com essa abordagem, com preprocessamento O(n log n), podemos responder queries de LCA (e climb, e dist) em O(log n), além disso, podemos modificar a DP do LCA para guardar mais informações além de qual o (2^k)-ésimo pai, por exemplo a aresta mínima(ou máxima) nesse caminho, a soma dos custos das arestas(caso hajam pesos), máximo divisor comum, etc.
Abordagem 2
A segunda abordagem usa uma ideia diferente, mas que também é muito top. Com preprocessamento O(n log n) podemos fazer queries de LCA em O(1). Parando pra pensar nisso, é muito poderoso, não importa o quanto seja o tamanho do grafo, teremos a resposta em tempo constante! A ideia para atingir essa complexidade é a seguinte. Sabemos que usando uma Sparse Table(Vide aula de Sparse Table) podemos resolver problemas de RMQ (range minimum query) em O(1), com preprocessamento O(n log n) a ideia é construir um vetor de forma que a RMQ nele representa a query de LCA.
Materiais complementares
https://www.youtube.com/watch?v=EKcQt-74bNw
Exercícios recomendados
- https://codeforces.com/problemset/problem/208/e
- https://www.urionlinejudge.com.br/judge/pt/problems/view/2470
- https://www.urionlinejudge.com.br/judge/pt/problems/view/1135
- https://www.spoj.com/problems/QTREE2/ - queries de distancia e obter k-ésimo vértice no caminho, Só da pra obter késimo vértice com LCA log.